题目内容
1.已知函数f(x)=x-alnx(a∈R).(1)求函数f(x)的极值.
(2)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程与曲线y2=x所围成图形面积.
分析 (1)求出函数的导函数,由导函数可知,当a≤0时,f′(x)>0,函数在定义域(0,+∝)上单调递增,函数无极值,当a>0时,求出导函数的零点,由导函数的零点对定义域分段,利用原函数的单调性得到函数的极值;
(2)把a=2代入原函数解析式中,求出函数在x=1时的导数值,直接利用直线方程的点斜式写直线方程,再由定积分公式,计算即可得到所求面积.
解答 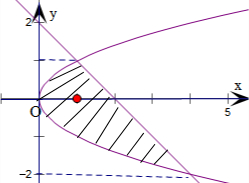 解:(1)由f′(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,x>0知:
解:(1)由f′(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,x>0知:
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a.
又当x∈(0,a)时,f′(x)<0,当x∈(a,+∞)时,f′(x)>0.
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-alna,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-alna,无极大值.
(2)当a=2时,f(x)=x-2lnx,f′(x)=1-$\frac{2}{x}$(x>0),
因而f(1)=1,f′(1)=-1,
所以曲线y=f(x)在点A(1,f(1))处的切线方程为
y-1=-(x-1),即x+y-2=0,
由y=2-x和解得交点坐标为(1,1),(4,-2),
则围成图形面积为${∫}_{-2}^{1}$(2-y-y2)dy=(2y-$\frac{1}{2}$y2-$\frac{1}{3}$y3)|${\;}_{-2}^{1}$
=(2-$\frac{1}{2}-\frac{1}{3}$)-(-4-2+$\frac{8}{3}$)=$\frac{9}{2}$.
点评 本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数研究函数的极值,考查了分类讨论的数学思想以及定积分的运用,属中档题.

| A. | 48 | B. | 72 | C. | 96 | D. | 144 |
| A. | y=sin2x | B. | y=x3-x | C. | y=xex | D. | y=-x+ln(1+x) |
| A. | 频率分布直方图中每个小矩形的高就是该组的频率 | |
| B. | 频率分布直方图中各个小矩形的面积之和等于1 | |
| C. | 频率分布直方图中各个小矩形的宽一样大 | |
| D. | 频率分布折线图是依次连接频率分布直方图的每个小矩形上端中点得到的 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 一$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |