题目内容
11.cos17°sin43°+sin17°sin47°( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 一$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 由诱导公式可得sin47°=cos43°,可得原式=cos17°sin43°+sin17°cos43°,由两角和的正弦公式可得.
解答 解:由诱导公式可得sin47°=sin(90°-43°)=cos43°,
∴cos17°sin43°+sin17°sin47°
=cos17°sin43°+sin17°cos43°
=sin(43°+17°)=sin60°=$\frac{\sqrt{3}}{2}$
故选:B.
点评 本题考查两角和的正弦公式,涉及诱导公式的应用,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.设m,n表示两条不同直线,α,β表示两个不同的平面,下列说法正确的是( )
| A. | 若m∥β,β⊥α则m⊥α | B. | 若m⊥n,n⊥β,β⊥α,则m⊥α | ||
| C. | 若m⊥α,m⊥n则n∥α | D. | 若m⊥α,n?α,则m⊥n |
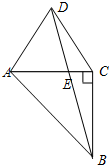 如图所示,△ACD是边长为1的等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于点E.则线段AE的长为$\sqrt{3}$-1.
如图所示,△ACD是边长为1的等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于点E.则线段AE的长为$\sqrt{3}$-1.