题目内容
7.设点A,B的坐标分别为(-a,0),(a,0),直线AC,BC相交于点C,且它们的斜率之积是-$\frac{{b}^{2}}{{a}^{2}}$(常数a,b为正实数).(Ⅰ)求点C的轨迹E的方程;
(Ⅱ)设O为坐标原点,P,Q为轨迹E上的动点,且OP⊥OQ,求$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$的值.
分析 (Ⅰ)利用直接法求点C的轨迹E的方程;
(Ⅱ)设P(ρ1,θ),Q(ρ2,θ+$\frac{π}{2}$),利用极坐标方程求:$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$的值.
解答 解:(Ⅰ)设C(x,y),则由题意可得$\frac{y}{x+a}•\frac{y}{x-a}$=-$\frac{{b}^{2}}{{a}^{2}}$,
化简可得$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$;
(Ⅱ)$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$化为极坐标方程$\frac{1}{{ρ}^{2}}$=$\frac{co{s}^{2}θ}{{a}^{2}}+\frac{si{n}^{2}θ}{{b}^{2}}$
设P(ρ1,θ),Q(ρ2,θ+$\frac{π}{2}$),
∴$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{co{s}^{2}θ}{{a}^{2}}+\frac{si{n}^{2}θ}{{b}^{2}}$+$\frac{co{s}^{2}(θ+\frac{π}{2})}{{a}^{2}}+\frac{si{n}^{2}(θ+\frac{π}{2})}{{b}^{2}}$=$\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}$.
点评 本题考查轨迹方程,考查极坐标方程的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
14.已知函数f(x)(x∈R)是偶函数,函数f(x-2)是奇函数,且f(1)=1,则f(2015)=( )
| A. | 2015 | B. | -2015 | C. | 1 | D. | -1 |
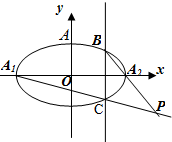 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.