题目内容
15.已知△ABC是等边三角形,有一点D满足$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{AC}$=$\overrightarrow{AD}$,且|$\overrightarrow{CD}$|=$\sqrt{3}$,那么$\overrightarrow{DA}$•$\overrightarrow{DC}$=3.分析 由已知画出图形,得到各向量的关系,求出等边三角形的边长,利用数量积公式解答.
解答 解:由已知得到如图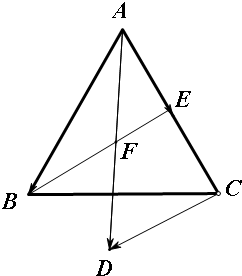
因为△ABC是等边三角形,有一点D满足$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{AC}$=$\overrightarrow{AD}$,且|$\overrightarrow{CD}$|=$\sqrt{3}$,
所以EF∥CD,并且EF=$\frac{\sqrt{3}}{2}$,所以BE=$\sqrt{3}$,AC=2,
所以AD=$\sqrt{A{C}^{2}+C{D}^{2}}=\sqrt{7}$,
$\overrightarrow{DA}$•$\overrightarrow{DC}$=|$\overrightarrow{DA}$||$\overrightarrow{DC}$|cosD=$\sqrt{7}×\sqrt{3}×\frac{CD}{AD}$=$\sqrt{7}×\sqrt{3}×\frac{\sqrt{3}}{\sqrt{7}}$=3;
故答案为:3.
点评 本题考查了平面向量的三角形法则以及数量积公式的运用,属于基础题.

练习册系列答案
相关题目
20.函数y=ax+1-3(a>0,a≠1)过定点A,若点A在直线mx+ny=-2(m>0,n>0)上,则$\frac{1}{m}$+$\frac{1}{n}$的最小值为( )
| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{3-2\sqrt{2}}{3}$ |