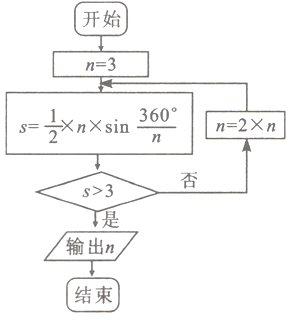
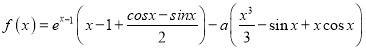题目内容
【题目】如图,在△ABC中,∠B=![]() ,AB=8,点D在BC边上,CD=2,cos∠ADC=
,AB=8,点D在BC边上,CD=2,cos∠ADC=![]() .
.
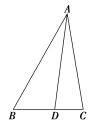
(1)求sin∠BAD;
(2)求BD,AC的长.
【答案】(1)![]() (2)
(2)![]() ,AC=7.
,AC=7.
【解析】
(1)根据sin∠BAD=sin(∠ADC-∠B),利用和差公式求解;
(2)在△ABD中,利用正弦定理即可求解BD,在△ABC中结合余弦定理求解.
(1)在△ADC中,因为cos∠ADC=![]() ,所以sin∠ADC=
,所以sin∠ADC=![]() .
.
所以sin∠BAD=sin(∠ADC-∠B)
=sin∠ADC cos B-cos∠ADC sin B
=![]()
![]() .
.
(2)在△ABD中,由正弦定理,得
BD=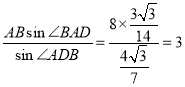 .
.
在△ABC中,由余弦定理,得
AC2=AB2+BC2-2AB×BC×cos B
=82+52-2×8×5×![]() =49.
=49.
所以AC=7.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】罗马数字是欧洲在阿拉伯数字传入之前使用的一种数码,它的产生标志着一种古代文明的进步.罗马数字的表示法如下:
数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
形式 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ | Ⅸ |
其中“Ⅰ”需要1根火柴,“Ⅴ”与“X”需要2根火柴,若为0,则用空位表示. (如123表示为![]() ,405表示为
,405表示为![]() )如果把6根火柴以适当的方式全部放入下面的表格中,那么可以表示的不同的三位数的个数为( )
)如果把6根火柴以适当的方式全部放入下面的表格中,那么可以表示的不同的三位数的个数为( )
![]()
A.87B.95C.100D.103