题目内容
13.在△ABC中,角A、B、C所对的边分别是a、b、c,若$({a^2}+{c^2}-{b^2})tanB=\sqrt{3}ac$,则$\frac{bsinA}{a}$的值为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由余弦定理化简条件得2ac•cosB•tanB=ac,再根据同角三角函数的基本关系得 sinB=$\frac{\sqrt{3}}{2}$,从而求得角B的值.
解答 解:∵在△ABC中,角A、B、C的对边分别为a、b、c,(a2+c2-b2)tanB=$\sqrt{3}$ac,
∴2ac•cosB•tanB=$\sqrt{3}$ac,
∴sinB=$\frac{\sqrt{3}}{2}$,
∴由正弦定理可得:$\frac{bsinA}{a}$=sinB=$\frac{\sqrt{3}}{2}$,
故选:D.
点评 本题考查余弦定理的应用,同角三角函数的基本关系,以及根据三角函数值及角的范围求角的大小.

练习册系列答案
相关题目
3.函数f(x)=$\frac{{a}^{x+1}+{b}^{x+1}}{{a}^{x}+{b}^{x}}$(a>0,b>0,a≠b)在R上的单调性为( )
| A. | 增函数 | B. | 减函数 | C. | 不增不减函数 | D. | 与a,b的取值有关 |
3.在空间四边形OABC中,M为BC的中点,N为OM的中点,连接AC,则向量$\overrightarrow{AO}+\frac{1}{2}$($\overrightarrow{AB}+\overrightarrow{AC}$)化简后的结果为( )
| A. | $\overrightarrow{ON}$ | B. | $\overrightarrow{AM}$ | C. | $\overrightarrow{AN}$ | D. | 2$\overrightarrow{AN}$ |
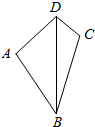 如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.
如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.