��Ŀ����
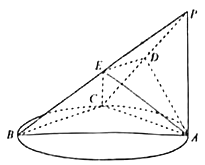
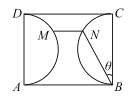
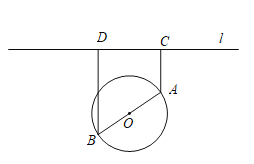
����Ŀ����ͼ��һ�����ı߽���Բ��ΪO��Բ������һ����һ��ֱ����·l����������AB��AB��ԲO��ֱ�������滮�ڹ�·l��ѡ������P��Q����������ֱ���͵�·PB��QA���滮Ҫ��:�߶�PB��QA�ϵ����е㵽��O�ľ������С��ԲO�İ뾶����֪��A��B��ֱ��l�ľ���ֱ�ΪAC��BD��C��DΪ���㣩�����AB=10��AC=6��BD=12����λ:���ף���
��1������·PB����AB��ֱ�����·PB�ij���
��2���ڹ滮Ҫ���£�P��Q���ܷ���һ����ѡ��D������˵�����ɣ�
��3���Թ滮Ҫ���£�����·PB��QA�ij��Ⱦ�Ϊd����λ�����ף�.��d��Сʱ��P��Q�����ľ��룮
���𰸡���1��15�����ף���
��2����������
��3��17+![]() �����ף�.
�����ף�.
��������
�⣺�ⷨһ��
��1����A��![]() ������ΪE.���ü��ι�ϵ������õ�·PB�ij���
������ΪE.���ü��ι�ϵ������õ�·PB�ij���
��2����������P��Q���ܷ���һ����ѡ��D������.
��3�������۵�P��λ�ã�Ȼ�������۵�Q��λ�ü���ȷ����d��Сʱ��P��Q�����ľ��룮
�ⷨ����
��1�������ռ�ֱ������ϵ���ֱ�ȷ����P�͵�B�����꣬Ȼ����������֮����빫ʽ�ɵõ�·PB�ij���
��2����������P��Q���ܷ���һ����ѡ��D������.
��3�������۵�P��λ�ã�Ȼ�������۵�Q��λ�ü���ȷ����d��Сʱ��P��Q�����ľ��룮
�ⷨһ��
��1����A��![]() ������ΪE.
������ΪE.
����֪�����ã��ı���ACDEΪ���Σ�![]() .
.
��ΪPB��AB��
����![]() .
.
����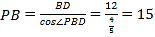 .
.
��˵�·PB�ij�Ϊ15�����ף�.
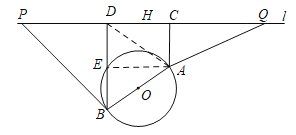
��2������P��D�����ɣ�1���ɵ�E��Բ�ϣ����߶�BE�ϵĵ㣨��B��E������O�ľ����С��ԲO�İ뾶������Pѡ��D��������滮Ҫ��.
����Q��D��������AD���ɣ�1��֪![]() ��
��
�Ӷ�![]() �����ԡ�BADΪ���.
�����ԡ�BADΪ���.
�����߶�AD�ϴ��ڵ㵽��O�ľ���С��ԲO�İ뾶.
��ˣ�Qѡ��D��Ҳ������滮Ҫ��.
���ϣ�P��Q������ѡ��D��.
��3�������۵�P��λ��.
����OBP<90��ʱ���߶�PB�ϴ��ڵ㵽��O�ľ���С��ԲO�İ뾶����P�����Ϲ滮Ҫ��
����OBP��90��ʱ�����߶�PB������һ��F��OF��OB�����߶�PB�����е㵽��O�ľ������С��ԲO�İ뾶����P���Ϲ滮Ҫ��.
��![]() Ϊl��һ�㣬��
Ϊl��һ�㣬��![]() ���ɣ�1��֪��
���ɣ�1��֪��![]() ��
��
��ʱ![]() ��
��
����OBP>90��ʱ����![]() �У�
�У�![]() .
.
���Ͽ�֪��d��15.
�����۵�Q��λ��.
�ɣ�2��֪��Ҫʹ��QA��15����Qֻ��λ�ڵ�C���Ҳ࣬���ܷ��Ϲ滮Ҫ��.��QA=15ʱ��![]() .��ʱ���߶�QA�����е㵽��O�ľ������С��ԲO�İ뾶.
.��ʱ���߶�QA�����е㵽��O�ľ������С��ԲO�İ뾶.
���ϣ���PB��AB����Qλ�ڵ�C�Ҳ࣬��CQ=![]() ʱ��d��С����ʱP��Q�����ľ���PQ=PD+CD+CQ=17+
ʱ��d��С����ʱP��Q�����ľ���PQ=PD+CD+CQ=17+![]() .
.
��ˣ�d��Сʱ��P��Q�����ľ���Ϊ17+![]() �����ף�.
�����ף�.
�ⷨ����
��1����ͼ����O��OH��l������ΪH.
��OΪ����ԭ�㣬ֱ��OHΪy�ᣬ����ƽ��ֱ������ϵ.
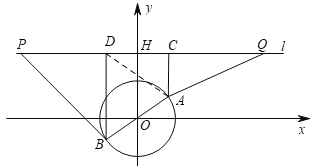
��ΪBD=12��AC=6������OH=9��ֱ��l�ķ���Ϊy=9����A��B��������ֱ�Ϊ3��3.
��ΪABΪԲO��ֱ����AB=10������ԲO�ķ���Ϊx2+y2=25.
�Ӷ�A��4��3����B��4��3����ֱ��AB��б��Ϊ![]() .
.
��ΪPB��AB������ֱ��PB��б��Ϊ![]() ��
��
ֱ��PB�ķ���Ϊ![]() .
.
����P��13��9����![]() .
.
��˵�·PB�ij�Ϊ15�����ף�.
��2������P��D����ȡ�߶�BD��һ��E��4��0������EO=4<5������Pѡ��D��������滮Ҫ��.
����Q��D��������AD���ɣ�1��֪D��4��9������A��4��3����
�����߶�AD��![]() .
.
���߶�AD��ȡ��M��3��![]() ������Ϊ
������Ϊ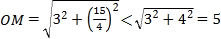 ��
��
�����߶�AD�ϴ��ڵ㵽��O�ľ���С��ԲO�İ뾶.
���Qѡ��D��Ҳ������滮Ҫ��.
���ϣ�P��Q������ѡ��D��.
��3�������۵�P��λ��.
����OBP<90��ʱ���߶�PB�ϴ��ڵ㵽��O�ľ���С��ԲO�İ뾶����P�����Ϲ滮Ҫ��
����OBP��90��ʱ�����߶�PB������һ��F��OF��OB�����߶�PB�����е㵽��O�ľ������С��ԲO�İ뾶����P���Ϲ滮Ҫ��.
��![]() Ϊl��һ�㣬��
Ϊl��һ�㣬��![]() ���ɣ�1��֪��
���ɣ�1��֪��![]() ����ʱ
����ʱ![]() ��
��
����OBP>90��ʱ����![]() �У�
�У�![]() .
.
���Ͽ�֪��d��15.
�����۵�Q��λ��.
�ɣ�2��֪��Ҫʹ��QA��15����Qֻ��λ�ڵ�C���Ҳ࣬���ܷ��Ϲ滮Ҫ��.
��QA=15ʱ����Q��a��9������![]() ��
��
��a=![]() ������Q��
������Q��![]() ��9������ʱ���߶�QA�����е㵽��O�ľ������С��ԲO�İ뾶.
��9������ʱ���߶�QA�����е㵽��O�ľ������С��ԲO�İ뾶.
���ϣ���P��13��9����Q��![]() ��9��ʱ��d��С����ʱP��Q�����ľ���
��9��ʱ��d��С����ʱP��Q�����ľ���
![]() .
.
��ˣ�d��Сʱ��P��Q�����ľ���Ϊ![]() �����ף�.
�����ף�.

����Ŀ��ijУΪ�˽�У��ȫ����ϵ�л�ij�Ч����ȫУѧ��������һ�ΰ�ȫ��ʶ���ԣ����ݲ��Գɼ��������ϸ������ϸ������ȼ���ͬʱ����Ӧ�ȼ��������������ϸ�5�֣������ϸ�0��.�������ȡ����ѧ���Ĵ����ͳ�ƽ������Ӧ��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
�ȼ� | ���ϸ� | �ϸ� | ||
�÷� |
|
|
|
|
Ƶ�� | 6 |
| 24 |
|
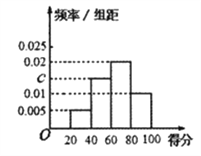
������![]() ��
�� ![]() ��
�� ![]() ��ֵ��
��ֵ��
�����÷ֲ�����ķ������������ȼ�Ϊ���ϸ͡����ϸ�ѧ���������ȡ10�˽�����̸.���ٴ���10������ѡ4�ˣ�����ѡ4�˵������ܷ�Ϊ![]() ����
����![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() ��
��
����ij����������ָ��![]() ��
��![]() ������
������![]() ��ʾ
��ʾ![]() �ķ����������У��ȫ������ij�Ч.��
�ķ����������У��ȫ������ij�Ч.��![]() �����϶����������Ч�ģ������϶��������Ч��Ӧ������ȫ��������.�ڣ��������£��жϸ�У�Ƿ�Ӧ������ȫ����������
�����϶����������Ч�ģ������϶��������Ч��Ӧ������ȫ��������.�ڣ��������£��жϸ�У�Ƿ�Ӧ������ȫ����������