��Ŀ����
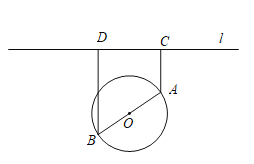
����Ŀ��ij�о���������һ����ҩ����ó���ע���ҩ��ѪҩŨ��y����/���������ҩʱ��x��Сʱ��֮������������ݣ����ɴ˵ó�y��x֮���һ����Ϻ���y��40��0.6x��0.62x����x��[0��12]�������ͼ��ͼ��ʾ.�Ը��ݴ���Ϻ�������������⣺

��1����ҩ��Ũ����ҩ��ʱ�䣨��ȷ��0.01Сʱ������ָ��ѪҩŨ����ʱ��ı仯���ƣ�
��2����ѪҩŨ�ȵİ�˥�ڣ�ѪҩŨ�ȴ�ҩ��Ũ�Ƚ�����һ������Ҫ��ʱ�䣩����ȷ��0.01Сʱ��.
���𰸡���1��ҩ��Ũ��Ϊ10��ҩ��ʱ��Ϊ1.36Сʱ��ע���ҩ��ѪҩŨ�������ӣ���1.36Сʱʱ�ﵽ��ֵ��Ȼ��ѪҩŨ�����ͣ���2��2.36Сʱ.
��������
��1��������Ϻ������û�Ԫ��������ֵ����ϵ����Կɵ�ѪҩŨ����ʱ��ı仯���ƣ�
��2�����ݰ�˥�ڵĺ���ⷽ�̿���.
��1����y��40��0.6x��0.62x����x��[0��12]����
��0.6x��t��t��[0.612��1]��
��y��40��0.6x��0.62x����40����t2+t����
�൱t![]() ��[0.612��1]����
��[0.612��1]����![]() ��x
��x![]() 1.36ʱ��
1.36ʱ��
y�����ֵΪ10.
��ҩ��Ũ��Ϊ10��ҩ��ʱ��Ϊ1.36Сʱ��
��ͼ���֪��ע���ҩ��ѪҩŨ�������ӣ���1.36Сʱʱ�ﵽ��ֵ��Ȼ��ѪҩŨ�����ͣ�
��2����y��40��0.6x��0.62x���У�ȡy��5����40��0.6x��0.62x����5��
����8t2+8t��1��0�����t![]() ��t
��t![]() ���ᣩ��
���ᣩ��
��![]() 0.147����x
0.147����x![]() 3.72.
3.72.
��ѪҩŨ�ȵİ�˥��Ϊ3.72��1.36��2.36Сʱ.

����Ŀ��������ҹ�2012����2018�����������ֵ����λ��������Ԫ�������ݣ�
��� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
��ݴ��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
����������ֵ ����λ��������Ԫ�� | 8.5 | 9.6 | 10.4 | 11 | 11.1 | 12.1 | 13.6 |
(1)�ӱ������ݿ�֪![]() ��
��![]() ��������Խ�ǿ�������
��������Խ�ǿ�������![]() Ϊ���ͱ���
Ϊ���ͱ���![]() ΪԤ�����������Իع鷽�̣�
ΪԤ�����������Իع鷽�̣�
(2)��֪����2018��Ĺ���������ֵԼΪ20.5������Ԫ����(1)�Ľ��ۣ�����ҹ��������Ǹ���ݲ��ܸ�������2018��Ĺ���������ֵ��
�ο����ݣ�![]() ��
��
�ο���ʽ���ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ:
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ:
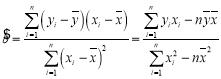 ��
��![]() .
.