ЬтФПФкШн
ЁОЬтФПЁПФГаЃЮЊСЫНтаЃдААВШЋНЬг§ЯЕСаЛюЖЏЕФГЩаЇЃЌЖдШЋаЃбЇЩњНјааСЫвЛДЮАВШЋвтЪЖВтЪдЃЌИљОнВтЪдГЩМЈЦРЖЈЁАКЯИёЁБЁЂЁАВЛКЯИёЁБСНИіЕШМЖЃЌЭЌЪБЖдЯргІЕШМЖНјааСПЛЏЃКЁАКЯИёЁБМЧ5ЗжЃЌЁАВЛКЯИёЁБМЧ0Зж.ЯжЫцЛњГщШЁВПЗжбЇЩњЕФД№ОэЃЌЭГМЦНсЙћМАЖдгІЕФЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃК
ЕШМЖ | ВЛКЯИё | КЯИё | ||
ЕУЗж |
|
|
|
|
ЦЕЪ§ | 6 |
| 24 |
|
ЃЈЂёЃЉЧѓ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉгУЗжВуГщбљЕФЗНЗЈЃЌДгЦРЖЈЕШМЖЮЊЁАКЯИёЁБКЭЁАВЛКЯИёЁБЕФбЇЩњжаЫцЛњГщШЁ10ШЫНјаазљЬИ.ЯждйДгет10ШЫетШЮбЁ4ШЫЃЌМЧЫљбЁ4ШЫЕФСПЛЏзмЗжЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаМАЪ§бЇЦкЭћ
ЕФЗжВМСаМАЪ§бЇЦкЭћ![]() ЃЛ
ЃЛ
ЃЈЂѓЃЉФГЦРЙРЛњЙЙвджИБъ![]() ЃЈ
ЃЈ![]() ЃЌЦфжа
ЃЌЦфжа![]() БэЪО
БэЪО![]() ЕФЗНВюЃЉРДЦРЙРИУаЃАВШЋНЬг§ЛюЖЏЕФГЩаЇ.Шє
ЕФЗНВюЃЉРДЦРЙРИУаЃАВШЋНЬг§ЛюЖЏЕФГЩаЇ.Шє![]() ЃЌдђШЯЖЈНЬг§ЛюЖЏЪЧгааЇЕФЃЛЗёдђШЯЖЈНЬг§ЛюЖЏЮоаЇЃЌгІЕїећАВШЋНЬг§ЗНАИ.дкЃЈЂђЃЉЕФЬѕМўЯТЃЌХаЖЯИУаЃЪЧЗёгІЕїећАВШЋНЬг§ЗНАИЃП
ЃЌдђШЯЖЈНЬг§ЛюЖЏЪЧгааЇЕФЃЛЗёдђШЯЖЈНЬг§ЛюЖЏЮоаЇЃЌгІЕїећАВШЋНЬг§ЗНАИ.дкЃЈЂђЃЉЕФЬѕМўЯТЃЌХаЖЯИУаЃЪЧЗёгІЕїећАВШЋНЬг§ЗНАИЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ ![]() ЃЛЃЈ2ЃЉЃЈ3ЃЉМћНтЮі.
ЃЛЃЈ2ЃЉЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУЦЕТЪЗжВМжБЗНЭМЕФаджЪМДПЩЕУГіЃЛЃЈ2ЃЉДгЦРЖЈЕШМЖЮЊЁАКЯИёЁБКЭЁАВЛКЯИёЁБЕФбЇЩњжаЫцЛњГщШЁ10ШЫНјаазљЬИЃЌЦфжаЁАВЛКЯИёЁБЕФбЇЩњ![]() ЃЌдђЁАКЯИёЁБЕФбЇЩњЪ§=6ЃЎгЩЬтвтПЩЕУІЮ=0ЃЌ5ЃЌ10ЃЌ15ЃЌ20ЃЎРћгУЁАГЌМИКЮЗжВМСаЁБЕФМЦЫуЙЋЪНМДПЩЕУГіИХТЪЃЌНјЖјЕУГіЗжВМСагыЪ§бЇЦкЭћЃЛЃЈ3ЃЉРћгУDІЮМЦЫуЙЋЪНМДПЩЕУГіЃЌПЩЕУ
ЃЌдђЁАКЯИёЁБЕФбЇЩњЪ§=6ЃЎгЩЬтвтПЩЕУІЮ=0ЃЌ5ЃЌ10ЃЌ15ЃЌ20ЃЎРћгУЁАГЌМИКЮЗжВМСаЁБЕФМЦЫуЙЋЪНМДПЩЕУГіИХТЪЃЌНјЖјЕУГіЗжВМСагыЪ§бЇЦкЭћЃЛЃЈ3ЃЉРћгУDІЮМЦЫуЙЋЪНМДПЩЕУГіЃЌПЩЕУ![]() ,МДПЩЕУГіНсТлЃЎ
,МДПЩЕУГіНсТлЃЎ
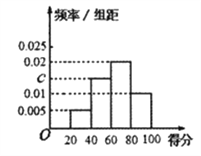
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМПЩжЊЃЌЕУЗждк![]() ЕФЦЕТЪЮЊ
ЕФЦЕТЪЮЊ![]() ЃЌ
ЃЌ
ЙЪГщШЁЕФбЇЩњД№ОэЪ§ЮЊЃК ![]() ЃЌ
ЃЌ
гжгЩЦЕТЪЗжВМжБЗНЭМПЩжЊЃЌЕУЗждк![]() ЕФЦЕТЪЮЊ0.2ЃЌ
ЕФЦЕТЪЮЊ0.2ЃЌ
Ыљвд![]() ЃЌ
ЃЌ
гж![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
Ыљвд![]() .
.
![]() .
.
ЃЈ2ЃЉЁАВЛКЯИёЁБгыЁАКЯИёЁБЕФШЫЪ§БШР§ЮЊ24ЃК36=2ЃК3ЃЌ
вђДЫГщШЁЕФ10ШЫжаЁАВЛКЯИёЁБга4ШЫЃЌЁАКЯИёЁБга6ШЫ.
Ыљвд![]() га20ЃЌ15ЃЌ10ЃЌ5ЃЌ0ЙВ5жжПЩФмЕФШЁжЕ.
га20ЃЌ15ЃЌ10ЃЌ5ЃЌ0ЙВ5жжПЩФмЕФШЁжЕ.
![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
![]() ЃЌ
ЃЌ ![]() .
.
![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 20 | 15 | 10 | 5 | 0 |
|
|
|
|
|
|
Ыљвд![]() .
.
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩЕУ
![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ
ЙЪЮвУЧШЯЮЊИУаЃЕФАВШЋНЬг§ЛюЖЏЪЧгааЇЕФЃЌВЛашвЊЕїећАВШЋНЬг§ЗНАИ.