题目内容
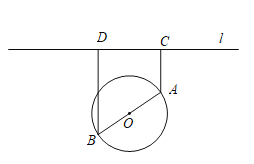
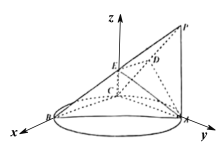
【题目】如图,点C在以AB为直径的圆上运动,PA⊥平面ABC,且PA=AC,D,E分别是PC,PB的中点.
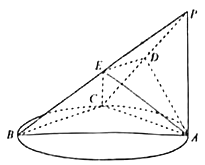
(1)求证:PC⊥平面ADE.
(2)若二面角C﹣AE﹣B为60°,求直线AB与平面ADE所成角的大小.
【答案】(1)见解析(2)30°.
【解析】
(1)由已知可得BC⊥平面PAC,进而有DE⊥平面PAC,可得DE⊥PC,再由已知可得AD⊥PC,即可证明结论;
(2)设PA=AC=1,设BC=t,建立以C为原点,CB为x轴,CA为y轴,过点C作![]() 的平行线为z轴,建立空间直角坐标系,求出平面ACE的法向量和平面ABE的法向量,结合已知求出
的平行线为z轴,建立空间直角坐标系,求出平面ACE的法向量和平面ABE的法向量,结合已知求出![]() ,求出
,求出![]() 坐标,用线面角公式即可求解.
坐标,用线面角公式即可求解.
(1)证明:∵点C在以AB为直径的圆上运动,PA⊥平面ABC,
∴BC⊥PA,BC⊥AC,∵AC∩PA=A,∴BC⊥平面PAC,
∵D,E分别是PC,PB的中点,∴DE∥BC,
∴DE⊥平面PAC,又PC平面PAC,∴DE⊥PC,
∵PA=AC,D是PC中点,∴AD⊥PC,
∵DE∩AD=D,∴PC⊥平面ADE.
(2)以C为原点,CB为x轴,CA为y轴,
过点C作![]() 的平行线为z轴,建立空间直角坐标系,
的平行线为z轴,建立空间直角坐标系,
设PA=AC=1,设BC=t,则A(0,1,0),B(t,0,0),
C(0,0,0),P(0,1,1),E(![]() ),
),
![]() (t,﹣1,0),
(t,﹣1,0),![]() (0,﹣1,0),
(0,﹣1,0),![]() (
(![]() ,
,![]() ),
),
设平面ACE的法向量![]() (x,y,z),
(x,y,z),
则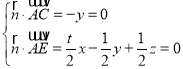 ,取x=1,得
,取x=1,得![]() (1,0,﹣t),
(1,0,﹣t),
设平面ABE的法向量![]() (x,y,z),
(x,y,z),
则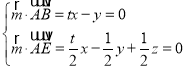 ,取x=1,得
,取x=1,得![]() (1,t,0),
(1,t,0),
∵二面角C﹣AE﹣B为60°,
∴cos60°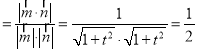 ,解得t=1,(t=﹣1,舍),
,解得t=1,(t=﹣1,舍),
∴B(1,0,0),![]() (﹣1,1,0),
(﹣1,1,0),
由(1)得![]() 为平面ADE的法向量
为平面ADE的法向量
设直线AB与平面ADE所成角的大小为θ,
则sinθ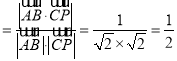 ,∴θ=30°,
,∴θ=30°,
∴直线AB与平面ADE所成角的大小为30°.

【题目】如表是我国2012年至2018年国内生产总值(单位:万亿美元)的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
国内生产总值 (单位:万亿美元) | 8.5 | 9.6 | 10.4 | 11 | 11.1 | 12.1 | 13.6 |
(1)从表中数据可知![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程;
为预报变量的线性回归方程;
(2)已知美国2018年的国内生产总值约为20.5万亿美元,用(1)的结论,求出我国最早在那个年份才能赶上美国2018年的国内生产总值?
参考数据:![]() ,
,
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
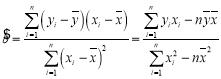 ,
,![]() .
.