Question

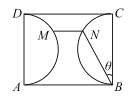
【题目】如图，某公园内有一块矩形绿地区域ABCD，已知AB=100米，BC=80米，以AD，BC为直径的两个半圆内种植花草，其它区域种值苗木. 现决定在绿地区域内修建由直路BN，MN和弧形路MD三部分组成的观赏道路，其中直路MN与绿地区域边界AB平行，直路为水泥路面，其工程造价为每米2a元，弧形路为鹅卵石路面，其工程造价为每米3a元，修建的总造价为W元. 设.

（1）求W关于的函数关系式；

（2）如何修建道路，可使修建的总造价最少？并求最少总造价.

Answer 1

【答案】(1) (2) 当时，修建的总造价最少，最少总造价为元

【解析】

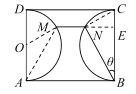
（1）连NC，AM，设AD的中点为O，连接MO，过N作，垂足为E.

可得，，从而得到W关于的函数关系式；

（2）利用导数知识研究函数的单调性与极值即可.

（1）连NC，AM，设AD的中点为O，连接MO，过N作，垂足为E.

由BC为直径知，，又米，，

所以米，，

因为MN∥AB，米，所以米，

由于米，

所以米，

因为直路的工程造价为每米2a元，弧形路的工程造价为每米3a元，

所以总造价为

,

，

.

所以W关于的函数关系式为

.

（2）记，

则

，

令，得，列表如下：

	—	0	+
		极小值

所以，当时，取得最小值，

此时，总造价W最少，最少总造价为元.

答：（1）W关于的函数关系式为

；

（2）当时，修建的总造价最少，最少总造价为元.