题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() ,(
,(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴的 非负半轴为极轴建立极坐标系,曲线
轴的 非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)![]() ;
;![]() (2)
(2)![]()
【解析】
(1)根据参数方程消去参数![]() 直接写出
直接写出![]() 的普通方程,利用
的普通方程,利用![]() 将
将![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)方法①:将![]() 的参数方程代入到
的参数方程代入到![]() 的直角坐标方程,根据
的直角坐标方程,根据![]() 的几何意义结合条件等式求解出
的几何意义结合条件等式求解出![]() 的值;
的值;
方法②:将![]() 的普通方程代入
的普通方程代入![]() 的直角坐标方程,根据韦达定理结合条件等式计算出
的直角坐标方程,根据韦达定理结合条件等式计算出![]() 的值即可.
的值即可.
(1)因为![]() 参数方程为
参数方程为![]() ,所以
,所以![]() 普通方程为:
普通方程为:![]() ,
,
因为![]() 的极坐标方程为
的极坐标方程为![]() ,所以
,所以![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(2)方法①:将曲线![]() 的参数方程化为
的参数方程化为 (
(![]() 为参数,
为参数,![]() ),
),
代入曲线![]() 得方程
得方程![]() ,
,
由![]() 得
得![]() ,
,
设点![]() 对应的参数分别为
对应的参数分别为![]() ,则
,则![]() 把上式代入
把上式代入 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() ,
,
而![]() ,故
,故![]() 为所求;
为所求;
方法②:将曲线![]() 代入曲线
代入曲线![]() 得方程
得方程![]() ,
,
由![]() 得
得![]() ,
,
设方程的两个根分别为![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,![]() ,
,
由题意得![]() ,即
,即![]() ,
,
把![]() ,
,![]() 代入
代入![]() ,
,
所以![]() ,
,
化简得![]() ,解得
,解得![]() ,此为所求.
,此为所求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如表是我国2012年至2018年国内生产总值(单位:万亿美元)的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
国内生产总值 (单位:万亿美元) | 8.5 | 9.6 | 10.4 | 11 | 11.1 | 12.1 | 13.6 |
(1)从表中数据可知![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程;
为预报变量的线性回归方程;
(2)已知美国2018年的国内生产总值约为20.5万亿美元,用(1)的结论,求出我国最早在那个年份才能赶上美国2018年的国内生产总值?
参考数据:![]() ,
,
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
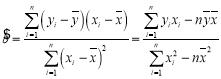 ,
,![]() .
.