题目内容
14.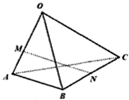 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )| A. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
分析 由题意,把$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$三个向量看作是基向量,由图形根据向量的线性运算,将$\overrightarrow{MN}$用三个基向量表示出来,即可得到答案,选出正确选项.
解答 解:$\overrightarrow{MN}$=$\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}$,
=$\frac{1}{3}$$\overrightarrow{OA}$+$\overrightarrow{OB}$-$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{BC}$,
=$-\frac{2}{3}$$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$-$\frac{1}{2}$$\overrightarrow{OB}$,
=-$\frac{2}{3}$$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$,
∵$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,
∴$\overrightarrow{MN}$=-$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$,
故选:A.
点评 本题考点是空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案| A. | A=150° | B. | A=120° | C. | A=60° | D. | A=30° |

| A. | i<99 | B. | i>99 | C. | i<100 | D. | i>100 |