题目内容
2.在△ABC中,若(a+b+c)(c+b-a)=bc,则A=( )| A. | A=150° | B. | A=120° | C. | A=60° | D. | A=30° |
分析 由条件里用余弦定理求得cosA的值,可得A的值.
解答 解:△ABC中,由(a+b+c)(c+b-a)=bc,可得b2+c2-a2=-bc,
∴cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$=-$\frac{1}{2}$,故A=120°,
故选:B.
点评 本题主要考查余弦定理的应用,根据三角函数的值求角,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知直线x-2y-2=0与直线x-2y+3=0,则它们之间的距离为( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |
14.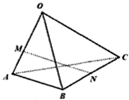 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )| A. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |

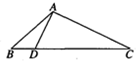 如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,求BD的长.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,求BD的长.