题目内容
9．在△ABC中，已知三边长是公差为1的等差数列，且最大角是最小角的两倍，求三边的长．分析 设△ABC中的三边长为a，a+1，a+2最小角，最小角和最大角为θ，2θ，分别由正弦定理和余弦定理，求出cosθ，解得即可．
解答 解：设△ABC中的三边长为a，a+1，a+2最小角，最小角和最大角为θ，2θ，
再由正弦定理可得$\frac{a}{sinθ}$=$\frac{a+2}{sin2θ}$，
所以cosθ=$\frac{a+2}{2a}$，
由余弦定理得cosθ=$\frac{（a+2）^{2}+（a+1）^{2}-{a}^{2}}{2（a+2）（a+1）}$=$\frac{a+2}{2a}$，解得a=4，
所以三边的长为4，5，6．
点评 本题主要考查等差数列的定义和性质，正弦定理、余弦定理，倍角公式的应用，属于中档题．
练习册系列答案
相关题目
如图，在圆心角为变量2θ（0＜2θ＜π）的扇形OAB内作一半径为r的内切圆P，再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q，圆P与圆Q相切于C点，圆P和圆Q与半径OA分别切于E，D两点．
14．
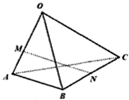如图，空间四边形OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在线段OA上，且OM=2MA，点N为BC的中点，则$\overrightarrow{MN}$=（ ）
如图，空间四边形OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在线段OA上，且OM=2MA，点N为BC的中点，则$\overrightarrow{MN}$=（ ）| A． | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$ | B． | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C． | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$ | D． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
1．已知数学、英语的成绩分别有优、良、及格、不及格四个档次，某班共60人，在每个档次的人数如表：
（1）求数学及格且英语良的概率；
（2）在数学及格的条件下，英语良的概率；
（3）若数学良与英语不及格是相互独立的，求a，b的值．
 | 优 | 良 | 及格 | 不及格 |
| 优 | 1 | 3 | 1 | 1 |
| 良 | 1 | 0 | 7 | 6 |
| 及格 | 2 | 4 | 0 | 9 |
| 不及格 | 1 | b | 7 | a+4 |
（2）在数学及格的条件下，英语良的概率；
（3）若数学良与英语不及格是相互独立的，求a，b的值．
18．
如图，在0～1随机选择两个数x，y，这两个数对应的点把0～1的线段分成了三条线段a，b，c，则这三条线段a，b，c能构成三角形的概率为（ ）
如图，在0～1随机选择两个数x，y，这两个数对应的点把0～1的线段分成了三条线段a，b，c，则这三条线段a，b，c能构成三角形的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |