题目内容
3.已知-$\frac{π}{2}$<x<0,sinx+cosx=$\frac{1}{5}$.(1)求sinx-cosx的值;
(2)求$\frac{3si{n}^{2}\frac{x}{2}-2sin\frac{x}{2}cos\frac{x}{2}+co{s}^{2}\frac{x}{2}}{tanx+tan(\frac{π}{2}-\frac{x}{2})}$的值.
分析 (1)已知等式两边平方,利用完全平方公式及同角三角函数间基本关系化简,整理求出2sinxcosx的值,再利用完全平方公式求出sinx-cosx的值即可;
(2)由sinx+cosx与sinx-cosx的值,联立求出sinx与cosx的值,进而求出sin$\frac{x}{2}$,cos$\frac{x}{2}$及tan$\frac{x}{2}$的值,原式化简后代入计算即可求出值.
解答 解:(1)∵-$\frac{π}{2}$<x<0,sinx+cosx=$\frac{1}{5}$①,
∴两边平方得:(sinx+cosx)2=1+2sinxcosx=$\frac{1}{25}$,即2sinxcosx=-$\frac{24}{25}$,
∴sinx<0,cosx>0,即sinx-cosx<0,
∵(sinx-cosx)2=1-2sinxcosx=$\frac{49}{25}$,
∴sinx-cosx=-$\frac{7}{5}$②;
(2)联立①②解得:sinx=-$\frac{3}{5}$,cosx=$\frac{4}{5}$,
∴1-2sin2$\frac{x}{2}$=$\frac{4}{5}$,即sin2$\frac{x}{2}$=$\frac{1}{10}$,
∵-$\frac{π}{4}$<$\frac{x}{2}$<0,∴sin$\frac{x}{2}$=$\frac{\sqrt{10}}{10}$,cos$\frac{x}{2}$=$\frac{3\sqrt{10}}{10}$,tan$\frac{x}{2}$=$\frac{1}{3}$,
则原式=$\frac{2si{n}^{2}\frac{x}{2}-sinx}{\frac{sinx}{cosx}+\frac{cos\frac{x}{2}}{sin\frac{x}{2}}}$=$\frac{\frac{1}{5}+\frac{3}{5}}{-\frac{3}{4}+3}$=$\frac{\frac{4}{5}}{\frac{9}{4}}$=$\frac{16}{45}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

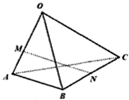 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )| A. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
 如图,在0~1随机选择两个数x,y,这两个数对应的点把0~1的线段分成了三条线段a,b,c,则这三条线段a,b,c能构成三角形的概率为( )
如图,在0~1随机选择两个数x,y,这两个数对应的点把0~1的线段分成了三条线段a,b,c,则这三条线段a,b,c能构成三角形的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
| 患病 | 未患病 | 总计 | |
| 服用药 | 15 | 40 | 55 |
| 没服用药 | 20 | 25 | 45 |
| 总计 | 35 | 65 | 100 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.025 | B. | 0.10 | C. | 0.01 | D. | 0.05 |