题目内容
4.解方程组:$\left\{\begin{array}{l}{{x}_{1}{-x}_{2}{+x}_{3}-{2x}_{4}=2}\\{{2x}_{1}{-x}_{3}+{4x}_{4}=4}\\{{3x}_{1}+{2x}_{2}{+x}_{3}=-1}\\{{-x}_{1}+{2x}_{2}{-x}_{3}+{2x}_{4}=-4}\end{array}\right.$.分析 将方程组消元,依次降为三元一次方程组,二元一次方程组和一元一次方程解之.
解答 解:方程①+④得x2=-2,
①+②得3x1-x2+2x4=6即3x1+2x4=4,⑤
②+③得5x1+2x2+4x4=3即5x1+4x4=7⑥
⑤×2-⑥得x1=1,
将x1=1,x2=-2代入③得3-4+x3=-1解得x3=0,
所以x4=$\frac{1}{2}$,
所以原方程组的解为:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{x}_{2}=-2}\\{{x}_{3}=0}\\{{x}_{4}=\frac{1}{2}}\end{array}\right.$.
点评 本题考查了多元方程组的解法;关键是观察方程组特点,正确消元.

练习册系列答案
相关题目
14.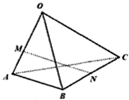 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )| A. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
9.设有编号为①,②,③,④,⑤的5个球和编号分别为1,2,3,4,5的5个盒子,现将这5个球放入这5个盒子内,要求每个盒内放1个球,并且盒子的编号与球的编号均不相同,则放球方法共有( )种.
| A. | 46 | B. | 44 | C. | 33 | D. | 45 |
6.为防止某种疾病,今研制一种新的预防药.任选取100只小白鼠作试验,得到如下的列联表:
经计算得K2的观测值为3.2079,则在犯错误的概率不超过( )的前提下认为“药物对防止某种疾病有效”.参考数据:
| 患病 | 未患病 | 总计 | |
| 服用药 | 15 | 40 | 55 |
| 没服用药 | 20 | 25 | 45 |
| 总计 | 35 | 65 | 100 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.025 | B. | 0.10 | C. | 0.01 | D. | 0.05 |