题目内容
5.一个均匀正四面体的4个面中,二个面上标以数0,一个面上标以数1,一个面上标以数2.将这个正四面体抛掷2次,其着地的一面上的数字之积的数学期望是$\frac{9}{16}$.分析 运用列表法求解(x,y)总共有16个基本事件,判断随机变量ξ=xy的数据ξ=0,1,2,4.根据古典概率求解即可.
解答 解:设x,y分别是第一次,第二次落地着地面的数值
∵x,y∈{0,0,1,2}
∴(x,y)总共有16个基本事件,
| (x,y) | 0 | 0 | 1 | 2 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 2 |
| 2 | 0 | 0 | 2 | 4 |
∴P(ξ=0)=$\frac{•12}{16}$=$\frac{3}{4}$,P(ξ=1)=$\frac{1}{16}$,P(ξ=2)=$\frac{2}{16}$=$\frac{1}{8}$,P(ξ=4)=$\frac{1}{16}$,
| ξ | 0 | 1 | 2 | 4 |
| P | $\frac{3}{4}$ | $\frac{1}{16}$ | $\frac{1}{8}$ | $\frac{1}{16}$ |
故答案为:$\frac{9}{16}$
点评 本题考查了古典概率的求解,关键是仔细阅读题意,运用表格的形式判断事件个数,考查了分析解决问题的能力.

练习册系列答案
相关题目
16.已知:x2+y2=2,则x-2y的最小值为( )
| A. | -$\sqrt{10}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{5}$ | D. | -$\sqrt{2}$ |
14.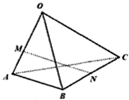 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在线段OA上,且OM=2MA,点N为BC的中点,则$\overrightarrow{MN}$=( )| A. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
 如图,在圆心角为变量2θ(0<2θ<π)的扇形OAB内作一半径为r的内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,圆P与圆Q相切于C点,圆P和圆Q与半径OA分别切于E,D两点.
如图,在圆心角为变量2θ(0<2θ<π)的扇形OAB内作一半径为r的内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,圆P与圆Q相切于C点,圆P和圆Q与半径OA分别切于E,D两点.