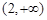题目内容
函数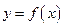 的图象与
的图象与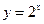 的图象关于直线
的图象关于直线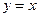 对称,则函数
对称,则函数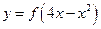 的递增区间是_________.
的递增区间是_________.
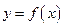 的图象与
的图象与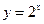 的图象关于直线
的图象关于直线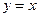 对称,则函数
对称,则函数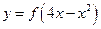 的递增区间是_________.
的递增区间是_________.(0,2)
∵函数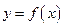 的图象与
的图象与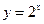 的图象关于直线
的图象关于直线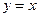 对称
对称
∴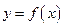 与
与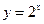 互为反函数
互为反函数
∵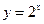 的反函数为
的反函数为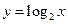 ,
,
∴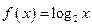 ,
,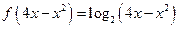 .
.
令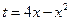 ,则
,则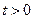 ,即
,即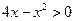 ,∴
,∴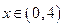 ,
,
又∵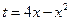 的对称轴为
的对称轴为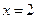 ,且对数的底数大于1,
,且对数的底数大于1,
∴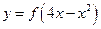 的递增区间为(0,2).
的递增区间为(0,2).
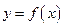 的图象与
的图象与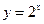 的图象关于直线
的图象关于直线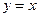 对称
对称∴
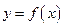 与
与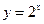 互为反函数
互为反函数∵
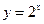 的反函数为
的反函数为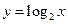 ,
,∴
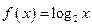 ,
,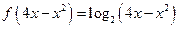 .
.令
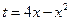 ,则
,则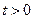 ,即
,即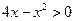 ,∴
,∴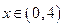 ,
,又∵
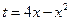 的对称轴为
的对称轴为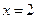 ,且对数的底数大于1,
,且对数的底数大于1,∴
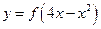 的递增区间为(0,2).
的递增区间为(0,2).
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
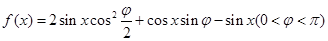 ,在
,在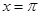 处取最小值.
处取最小值.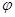 的值;
的值;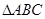 中,
中,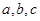 分别是
分别是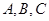 的对边,已知
的对边,已知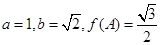 ,求角
,求角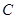 .
.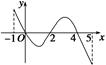
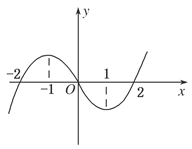
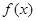 定义域为(0,+
定义域为(0,+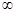 ),
),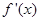 为
为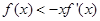 ,则不等式
,则不等式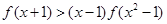 的解集是( )
的解集是( )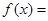
 则满足
则满足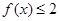 的
的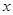 的取值范围是 .
的取值范围是 .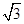 acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )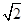
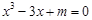 在
在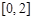 上有解,则实数
上有解,则实数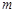 的取值范围是( )
的取值范围是( )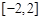
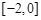
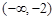 ∪
∪