题目内容
2.在平行四边形ABCD中,E,F分别是BC,CD的中点,DE交AF于点G,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AG}$=( )| A. | $\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ | B. | $\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | -$\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | D. | -$\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ |
分析 由题意画出图象,根据向量共线、向量的线性运算表示出$\overrightarrow{AG}$,列出方程组即可求出答案.
解答 解:由题意画出图象:
∵A、G、F三点共线,
∴$\overrightarrow{AG}=λ\overrightarrow{AF}$=$λ(\overrightarrow{AD}+\overrightarrow{DF})$=$λ(\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB})$=$λ(\overrightarrow{b}+\frac{1}{2}\overrightarrow{a})$,
同理可得,$\overrightarrow{DG}=μ\overrightarrow{DE}$=$μ(\overrightarrow{DC}+\overrightarrow{CE})$=$μ(\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD})$=$μ(\overrightarrow{a}-\frac{1}{2}\overrightarrow{b})$,
∵$\overrightarrow{AG}=\overrightarrow{AD}+\overrightarrow{DG}$=$\overrightarrow{b}$+$μ(\overrightarrow{a}-\frac{1}{2}\overrightarrow{b})$,
∴$\overrightarrow{b}+$$μ(\overrightarrow{a}-\frac{1}{2}\overrightarrow{b})$=$λ(\overrightarrow{b}+\frac{1}{2}\overrightarrow{a})$,
则$\left\{\begin{array}{l}{1-\frac{1}{2}μ=λ}\\{μ=\frac{1}{2}λ}\end{array}\right.$,解得λ=$\frac{4}{5}$,μ=$\frac{2}{5}$,
∴$\overrightarrow{AG}=\frac{4}{5}\overrightarrow{b}+\frac{2}{5}\overrightarrow{a}$,
故选:B.
点评 本题考查向量的线性运算,以及向量共线的条件,属于中档题.

| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(Ⅱ)若该次考试该班数学平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据:
$\sum_{i=1}^{8}$xiyi=20×6.5+15×3.5+13×3.5+3×1.5+2×0.5+(-5)×(-0.5)+(-10)×(-2.5)+(-18)×(-3.5)=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+(-5)2+(-10)2+(-18)2=1256.
| A. | 1 | B. | 2 | C. | sin1 | D. | 2sin1 |
(1)根据以上数据完成下面的2×2列联表.
| 喜欢网购 | 不喜欢网购 | 总计 | |
| 男职工 | |||
| 女职工 | |||
| 总计 |
参考数据及公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
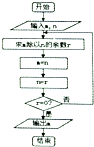 程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.
程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.