题目内容
13.在一次测量中,误差在±1%之内称为合格测量.某学生在一次测量中合格与否是等可能的.现对该学生的测量结果进行考核,共进行5次测量,记分规则如下表:| 合格次数 | 0~2 | 3 | 4 | 5 |
| 记分 | 0 | 3 | 6 | 10 |
(2)记ξ为该学生所得的分数,求ξ的分布列和数学期望.
分析 (1)由已知得该学生5次测量中的合格次数X~B(5,$\frac{1}{2}$),该学生得0分的概率P=P(X=0)+P(X=1)+P(X=2),由此能求出该学生得0分的概率.
(2)记ξ为该学生所得的分数,由已知得ξ的可能取值为0,3,6,10,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 解:(1)由已知得该学生5次测量中的合格次数X~B(5,$\frac{1}{2}$),
∴该学生得0分的概率P=P(X=0)+P(X=1)+P(X=2)
=${C}_{5}^{0}(\frac{1}{2})^{5}+{C}_{5}^{1}(\frac{1}{2})(\frac{1}{2})^{4}$+${C}_{5}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{3}$
=$\frac{1}{2}$.
(2)记ξ为该学生所得的分数,由已知得ξ的可能取值为0,3,6,10,
P(ξ=0)=P(X=0)+P(X=1)+P(X=2)=${C}_{5}^{0}(\frac{1}{2})^{5}+{C}_{5}^{1}(\frac{1}{2})(\frac{1}{2})^{4}$+${C}_{5}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{3}$=$\frac{1}{2}$.
P(ξ=3)=P(X=3)${C}_{5}^{3}(\frac{1}{2})^{3}(\frac{1}{2})^{2}$=$\frac{5}{16}$,
P(ξ=6)=P(X=4)=${C}_{5}^{4}(\frac{1}{2})^{4}(\frac{1}{2})$=$\frac{5}{32}$,
P(ξ=10)=P(X=5)=${C}_{5}^{5}(\frac{1}{2})^{5}$=$\frac{1}{32}$,
∴ξ的分布列为:
| ξ | 0 | 3 | 6 | 10 |
| P | $\frac{1}{2}$ | $\frac{5}{16}$ | $\frac{5}{32}$ | $\frac{1}{32}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

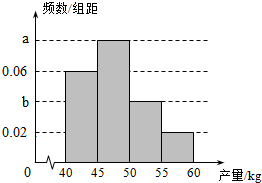 果农种了一片果树,收获时,果农随机随机选取果树20株作为样本.测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60],进行分组,得到频率分布直方图如图,已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.
果农种了一片果树,收获时,果农随机随机选取果树20株作为样本.测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60],进行分组,得到频率分布直方图如图,已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.(1)求a,b的值;
(2)果树的价格如下表:
| 产量 | (40,45] | (45,50] | (50,55] | (55,60] |
| 价格(百元/棵) | 1 | 2 | 3 | 4 |