题目内容
5.若实数x,y满足$\left\{\begin{array}{l}{x+2y≥2}\\{x≤2}\\{y≤1}\end{array}\right.$,则(x-1)2+y2的最小值为$\frac{1}{5}$.分析 由题意画出图形,由点到直线的距离公式求得可行域内点与(1,0)距离最小值的平方得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x+2y≥2\\ x≤2\\ y≤1\end{array}\right.$作出可行域如图,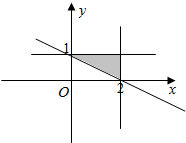
由图可知,(x-1)2+y2的最小值为坐标(1,0)到直线x+2y-2=0的距离的平方,
即($\frac{|1-2|}{\sqrt{{1}^{2}+{2}^{2}}}$)2=$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
17.函数y=3sin$\frac{x}{3}$+4cos$\frac{x}{3}$的最大值是( )
| A. | 5 | B. | -5 | C. | 6 | D. | -6 |
13.在一次测量中,误差在±1%之内称为合格测量.某学生在一次测量中合格与否是等可能的.现对该学生的测量结果进行考核,共进行5次测量,记分规则如下表:
(1)求该学生得0分的概率;
(2)记ξ为该学生所得的分数,求ξ的分布列和数学期望.
| 合格次数 | 0~2 | 3 | 4 | 5 |
| 记分 | 0 | 3 | 6 | 10 |
(2)记ξ为该学生所得的分数,求ξ的分布列和数学期望.
15.设函数f(x)满足f(n+1)=f(n)+$\frac{n}{2}$(n∈N*)且f (1)=2,则f (20)为( )
| A. | 95 | B. | 97 | C. | 105 | D. | 192 |