题目内容
6.函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2,x≥0}\\{{2}^{-x},x<0}\end{array}\right.$的反函数的定义域为(-∞,-2]∪(1,+∞).分析 求出原函数在不同区间上的值域,取并集得到原函数的值域,即其反函数的定义域.
解答 解:由f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2,x≥0}\\{{2}^{-x},x<0}\end{array}\right.$,
当x≥0时,f(x)=-x2-2≤-2;
当x<0时,f(x)=2-x>1.
∴函数f(x)的值域为(-∞,-2]∪(1,+∞).
即其反函数的定义域为:(-∞,-2]∪(1,+∞).
故答案为:(-∞,-2]∪(1,+∞).
点评 本题考查函数的反函数的定义域的求法,注意:函数的反函数的定义域,是原函数的值域,是基础题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
17.函数y=3sin$\frac{x}{3}$+4cos$\frac{x}{3}$的最大值是( )
| A. | 5 | B. | -5 | C. | 6 | D. | -6 |
14.函数y=$\frac{|tanx|}{tanx}$+$\frac{sinx}{|sinx|}$+$\frac{|cosx|}{cosx}$(x≠$\frac{kπ}{2}$,k∈Z)的值域是( )
| A. | {y|-1≤y≤3} | B. | {-3,-1,1,3} | C. | {y|-3≤y≤3} | D. | {-1,3} |
13.在一次测量中,误差在±1%之内称为合格测量.某学生在一次测量中合格与否是等可能的.现对该学生的测量结果进行考核,共进行5次测量,记分规则如下表:
(1)求该学生得0分的概率;
(2)记ξ为该学生所得的分数,求ξ的分布列和数学期望.
| 合格次数 | 0~2 | 3 | 4 | 5 |
| 记分 | 0 | 3 | 6 | 10 |
(2)记ξ为该学生所得的分数,求ξ的分布列和数学期望.
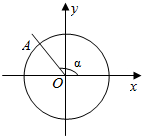 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的坐标是(cosα,$\frac{3}{5}$),则cosα-sinα=$-\frac{7}{5}$.
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的坐标是(cosα,$\frac{3}{5}$),则cosα-sinα=$-\frac{7}{5}$.