题目内容
3.若复数z满足$\frac{z}{1-i}$=i(i为虚数单位),则复数z对应点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由已知的复数方程求出复数z,找到对应点,确定位置.
解答 解:因为复数z满足$\frac{z}{1-i}$=i,所以z=i(1-i)=1+i,对应点为(1,1),所以复数z对应点在第一象限;
故选A.
点评 本题考查了复数的运算以及几何意义;正确解复数方程,明确对应点是关键.

练习册系列答案
相关题目
11.在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点M的直角坐标是(1,-$\sqrt{3}$),则点M的极坐标为( )
| A. | (2,-$\frac{π}{3}$) | B. | (2,$\frac{π}{3}$) | C. | (2,$\frac{2π}{3}$) | D. | (2,2kπ+$\frac{π}{3}$)(k∈Z) |
18.在直角坐标系xOy中,点M的坐标是(1,-$\sqrt{3}$),若以原点O为极点,x轴的非负半轴为极轴建立极坐标系,则点M的极坐标可以为( )
| A. | (2,$\frac{π}{3}$) | B. | (2,$\frac{2π}{3}$) | C. | (2,-$\frac{π}{3}$) | D. | (2,2kπ+$\frac{π}{3}$)(k∈Z) |
8.若直线y=kx+1与圆x2+y2=1相交与P,Q两点,且此圆被分成的两段弧长之比为1:2,则k的值为( )
| A. | $-\sqrt{3}$或$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\sqrt{2}$或$\sqrt{2}$ | D. | $\sqrt{2}$ |
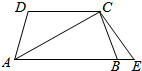 如图,在等腰梯形ABCD中,AB∥CD,延长AB到点E,使∠BEC=∠CAD.若AC=$\sqrt{2}$,CD=CE=1,则BC=$\frac{\sqrt{2}}{2}$.
如图,在等腰梯形ABCD中,AB∥CD,延长AB到点E,使∠BEC=∠CAD.若AC=$\sqrt{2}$,CD=CE=1,则BC=$\frac{\sqrt{2}}{2}$.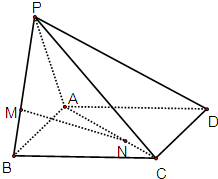 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,侧面PAB是边长为3的等边三角形,底面ABCD是正方形,M是侧棱PB上的点,N是底面对角线AC上的点,且PM=2MB,AN=2NC.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,侧面PAB是边长为3的等边三角形,底面ABCD是正方形,M是侧棱PB上的点,N是底面对角线AC上的点,且PM=2MB,AN=2NC.