题目内容
14.设函数f(x)=$\frac{1}{3}{x}^{3}$-ax,g(x)=bx2+2b-1.(Ⅰ)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(Ⅱ)当a=1-2b且a>0时,若函数f(x)+g(x)在区间(-2,0)内恰有两个零点,求a的取值范围.
分析 (Ⅰ)由题意求出f′(x)、g′(x),由题意得f(1)=g(1),且f′(1)=g′(1),解该方程组即可求出a、b的值;
(Ⅱ)把a=1-2b代入h(x)=f(x)+g(x)化简,并求出h′(x),利用导数求出单调性和极值,由函数在(-2,0)内有两零点列出不等式组,求出不等式的解集可得a的取值范围.
解答 解:(Ⅰ)由题意得,f′(x)=x2-a,g′(x)=2bx,
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,
所以f(1)=g(1),且f′(1)=g′(1),
则$\left\{\begin{array}{l}{\frac{1}{3}-a=3b-1}\\{1-a=2b}\end{array}\right.$,解得a=$\frac{1}{3}$,b=$\frac{1}{3}$;
(Ⅱ)记h(x)=f(x)+g(x),
当a=1-2b时,h(x)=$\frac{1}{3}{x}^{3}+\frac{1-a}{2}{x}^{2}-ax-a$,
则列出表格如下:
| x | (-∞,-1) | -1 | (-1,a) | a | (a,+∞) |
| h′(x) | + | 0 | - | 0 | + |
| h(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
故h(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,
从而函数h(x)在区间(-2,0)内恰有两个零点,当且仅当$\left\{\begin{array}{l}{h(-2)<0}\\{h(-1)>0}\\{h(0)<0}\end{array}\right.$,
解得$0<a<\frac{1}{3}$,
所以a的取值范围是(0,$\frac{1}{3}$).
点评 本题考查导数的几何意义,导数与函数的单调性、极值的关系,以及函数零点的条件应用,考查化简、变形能力,综合性大、难度大.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
4.已知集合A={0,1,2},集合B={-1,0,1},则集合A∩B=( )
| A. | {-1,0,1,2} | B. | {0,1} | C. | {-1,6} | D. | ∅ |
5.设a=logπ3,b=20.3,c=log2$\frac{1}{3}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | a>c>b |
3.若复数z满足$\frac{z}{1-i}$=i(i为虚数单位),则复数z对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
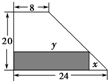 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12.
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12.