题目内容
11.在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点M的直角坐标是(1,-$\sqrt{3}$),则点M的极坐标为( )| A. | (2,-$\frac{π}{3}$) | B. | (2,$\frac{π}{3}$) | C. | (2,$\frac{2π}{3}$) | D. | (2,2kπ+$\frac{π}{3}$)(k∈Z) |
分析 利用$\left\{\begin{array}{l}{ρ=\sqrt{{x}^{2}+{y}^{2}}}\\{tanθ=\frac{y}{x}}\end{array}\right.$即可得出.
解答 解:∵$ρ=\sqrt{{1}^{2}+(-\sqrt{3})^{2}}$=2,$tanθ=-\sqrt{3}$,θ∈$(-\frac{π}{2},0)$,解得θ=$-\frac{π}{3}$.
∴点M的极坐标为$(2,-\frac{π}{3})$.
故选:A.
点评 本题考查了直角坐标化为极坐标的方法,属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
3.若复数z满足$\frac{z}{1-i}$=i(i为虚数单位),则复数z对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 (1)设实数x,y满足不等式组$\left\{\begin{array}{l}|{x+y-6}|≤2\\ y≤2x+4≤4y+4\end{array}\right.$,作出不等式组表示的平面区域,并求当a>0时,z=y-ax的最大值;
(1)设实数x,y满足不等式组$\left\{\begin{array}{l}|{x+y-6}|≤2\\ y≤2x+4≤4y+4\end{array}\right.$,作出不等式组表示的平面区域,并求当a>0时,z=y-ax的最大值;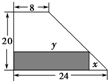 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12.
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12.