题目内容
15.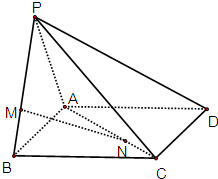 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,侧面PAB是边长为3的等边三角形,底面ABCD是正方形,M是侧棱PB上的点,N是底面对角线AC上的点,且PM=2MB,AN=2NC.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,侧面PAB是边长为3的等边三角形,底面ABCD是正方形,M是侧棱PB上的点,N是底面对角线AC上的点,且PM=2MB,AN=2NC.(Ⅰ)求证:AD⊥PB;
(Ⅱ)求证:MN∥平面PAD;
(Ⅲ)求点N到平面PAD的距离.
分析 (Ⅰ)证明AD⊥平面PAB,即可证明:AD⊥PB;
(Ⅱ)过M作MS∥BA交PA于点S,过N作NT∥CD交AD于点T,连接ST,证明MNTS是平行四边形,可得MN∥ST,即可证明MN∥平面PAD;
(Ⅲ)点M到平面PAD的距离是点N到平面PAD的距离.
解答 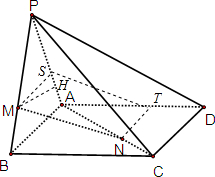 (Ⅰ)证明:∵侧面PAB⊥底面ABCD,且平面PAB与平面ABCD的交线为AB,AD⊥AB,AD?平面ABCD,
(Ⅰ)证明:∵侧面PAB⊥底面ABCD,且平面PAB与平面ABCD的交线为AB,AD⊥AB,AD?平面ABCD,
∴AD⊥平面PAB,
∵PB?平面PAB,∴AD⊥PB. …(3分)
(Ⅱ)证明:过M作MS∥BA交PA于点S,过N作NT∥CD交AD于点T,连接ST,
∵PM=2MB,
∴MS=$\frac{2}{3}$BA,
同理可得NT=$\frac{2}{3}$CD=$\frac{2}{3}$BA,
∴MS∥NT,MS=NT,
∴MNTS是平行四边形,
∴MN∥ST,
又ST?平面PAD,MN?平面PAD,
∴MN∥平面PAD.…(6分)
(Ⅲ)解:∵MN∥平面PAD,∴点M到平面PAD的距离是点N到平面PAD的距离,
在平面PAB内过M作MH⊥PA于H,
∵AD⊥平面PAB,∴AD⊥MH,
∴MH⊥平面PAD,
∴MH是点M到平面PAD的距离,
在Rt△PMH中,PM=2,∠MPH=$\frac{π}{3}$,∴$MH=\sqrt{3}$,
∴点N到平面PAD的距离为$\sqrt{3}$.…(9分)
点评 本题考查平面与平面垂直的性质、直线与平面垂直、平行的判定,考查点到平面距离的计算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设a=logπ3,b=20.3,c=log2$\frac{1}{3}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | a>c>b |
3.若复数z满足$\frac{z}{1-i}$=i(i为虚数单位),则复数z对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.已知直线过点A(m,m),B(m-1,m+1),则直线AB的倾斜角为( )
| A. | $\frac{π}{4}$ | B. | $-\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | 以m的值有关 |
7.下列四个函数中,以π为最小正周期,且在区间($\frac{π}{2}$,π)上为减函数的是( )
| A. | y=cosx | B. | y=|2sinx| | C. | y=cos$\frac{x}{2}$ | D. | y=tanx |