题目内容
8.若直线y=kx+1与圆x2+y2=1相交与P,Q两点,且此圆被分成的两段弧长之比为1:2,则k的值为( )| A. | $-\sqrt{3}$或$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\sqrt{2}$或$\sqrt{2}$ | D. | $\sqrt{2}$ |
分析 根据直线y=kx+1与圆x2+y2=1相交于P、Q两点,且∠POQ=120°(其中O为原点),求出圆心到直线的距离;再根据点到直线的距离公式即可求出k的值.
解答 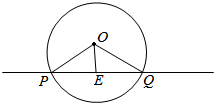 解:因为直线y=kx+1与圆x2+y2=1相交于P、Q两点,且此圆被分成的两段弧长之比为1:2,所以∠POQ=120°(其中O为原点),如图
解:因为直线y=kx+1与圆x2+y2=1相交于P、Q两点,且此圆被分成的两段弧长之比为1:2,所以∠POQ=120°(其中O为原点),如图
可得∠OPE=30°;OE=OPsin30°=$\frac{1}{2}$,
即圆心O(0,0)到直线y=kx+1的距离d=$\frac{1}{2}$=$\frac{|0-0+1|}{\sqrt{{k}^{2}+1}}$,
所以k=$±\sqrt{3}$.
故选:A.
点评 本题考查直线和圆的位置关系,点到直线的距离公式,考查计算能力,求出圆心(0,0)到直线的距离是解题的关键.

练习册系列答案
相关题目
18.设X为随机变量,X~B (n,$\frac{1}{3}$),若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
| A. | $\frac{80}{243}$ | B. | $\frac{13}{243}$ | C. | $\frac{4}{243}$ | D. | $\frac{13}{16}$ |
3.若复数z满足$\frac{z}{1-i}$=i(i为虚数单位),则复数z对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
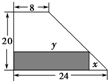 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12.
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12. 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,M为AD上一点且AM=2DM.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,M为AD上一点且AM=2DM.