题目内容
3.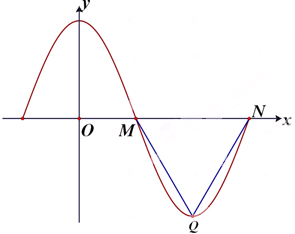 函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.
函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若f(x0+2)=$\sqrt{3}$,求sin$\frac{π}{4}$x0的值.
分析 (Ⅰ)由周期求得ω 的值,可得M(4,0)、N(12,0)、Q(8,-1).再利用等边三角形的性质求得A的值,可得f(x)的解析式.
(Ⅱ)由f(x0+2)=4$\sqrt{3}$cos($\frac{π}{8}$x0+$\frac{π}{4}$)=$\sqrt{3}$,求得cos($\frac{π}{8}$x0+$\frac{π}{4}$)的值,再根据sin$\frac{π}{4}$x0 =-cos($\frac{π}{4}$x0+$\frac{π}{2}$),利用二倍角的余弦公式计算求得结果.
解答 解:(Ⅰ)依题意有$\frac{3}{4}$T=$\frac{3}{4}$•$\frac{2π}{ω}$=12,∴T=16,ω=$\frac{π}{8}$,∴M(4,0)、N(12,0).
因为△MQN是等边三角形,所以|-A|=8•sin60°=4$\sqrt{3}$,∴A=4$\sqrt{3}$,Q(8,-4$\sqrt{3}$),f(x)=4$\sqrt{3}$cos$\frac{π}{8}$x.
(Ⅱ)∵f(x0+2)=4$\sqrt{3}$cos($\frac{π}{8}$x0+$\frac{π}{4}$)=$\sqrt{3}$,∴cos($\frac{π}{8}$x0+$\frac{π}{4}$)=$\frac{1}{4}$,
∴sin$\frac{π}{4}$x0 =-cos($\frac{π}{4}$x0+$\frac{π}{2}$)=-[2cos2($\frac{π}{8}$x0+$\frac{π}{4}$)-1]=$\frac{7}{8}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,余弦函数的图象特征,诱导公式、二倍角的余弦公式的应用,属于基础题.

| A. | 540 | B. | -162 | C. | 162 | D. | -540 |