题目内容
12.已知函数f(x)=lnx+$\frac{m}{x}$,m∈R.(1)若函数f(x)在(1,f(1))处的切线过点(0,3),求f(x)的解析式;
(2)若函数f(x)在[3,4)上单调递减,求实数m的取值范围;
(3)若函数f(x)在[1,e]上的最小值为$\frac{3}{2}$,求实数m的值.
分析 (1)求出函数的导数,求得切点,由点斜式方程可得切线方程,代入(0,3),可得m=2,进而得到函数解析式;
(2)求出导数,f(x)在[3,4)上是减函数,即为f′(x)≤0在[3,4)上恒成立,运用参数分离和求值域方法,即可得到所求范围;
(3)求出导数,对m讨论,①若m≤1,②若1<m<e,③若m≥e,判断在[1,e]的单调性,可得最小值,解方程即可得到m的值.
解答 解:(1)函数f(x)=lnx+$\frac{m}{x}$,f(1)=m,
由f′(x)=$\frac{1}{x}$-$\frac{m}{{x}^{2}}$,可得
f′(1)=1-m,
切线方程为y-m=(1-m)(x-1),
又因为切线过点(0,3),
所以3-m=(1-m)(0-1),解得m=2,
所以f(x)的解析式为f(x)=lnx+$\frac{2}{x}$.
(2)∵f′(x)=$\frac{1}{x}$-$\frac{m}{{x}^{2}}$,
∵f(x)在[3,4)上是减函数,
∴f′(x)≤0在[3,4)上恒成立,即m≥x在[3,4)上恒成立.
所以实数m的取值范围为[4,+∞).
(3)由(2)得f′(x)=$\frac{x-m}{{x}^{2}}$,x∈[1,e].
①若m≤1,则x-m≥0,即在[1,e]上f′(x)≥0恒成立,
此时f(x)在[1,e]上是增函数.
所以f(x)min=f(1)=m=$\frac{3}{2}$(舍去).
②若1<m<e,令f′(x)=0,得x=m.当1<x<m时,f′(x)<0,
所以f(x)在(1,m)上是减函数,当m<x<e时,f′(x)>0,
所以f(x)在(m,e)上是增函数.
所以f(x)min=f(m)=1+lnm=$\frac{3}{2}$,解得m=$\sqrt{e}$(符合要求).
③若m≥e,则x-m≥0,即f′(x)≤0在[1,e]上恒成立,
此时f(x)在[1,e]上是减函数.
所以f(x)min=f(e)=lne+$\frac{m}{e}$=$\frac{3}{2}$,所以m=$\frac{1}{2}$e(舍去).
综上所述m=$\sqrt{e}$.
点评 本题考查导数的运用:求切线方程和单调区间以及最值,主要考查导数的几何意义和函数的单调性的运用,运用分类讨论的思想方法是解题的关键.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案| A. | (-∞,-2] | B. | (-∞,-1] | C. | [0,+∞) | D. | [1,+∞) |
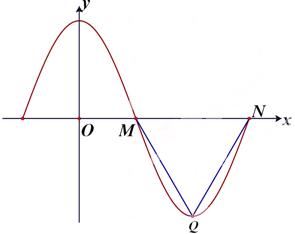 函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.
函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.