已知函数f(x)是定义在R上的奇函数.且当x＞0时.fx．的解析式,(2)画出函数的图象.根据图象写出函数f(x)的单调区间．题目和参考答案——青夏教育精英家教网——

题目内容

18．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=（

\frac{1}{2}

$\frac{1}{2}$ ）^x．
（1）求函数f（x）的解析式；
（2）画出函数的图象，根据图象写出函数f（x）的单调区间．

分析（1）当x＜0时，-x＞0，由奇函数可得此时解析式，又可得f（0）=0，综合可得；
（2）由分段函数解析式可得图象，可得单调递减区间．

解答解：（1）∵f（x）是定义在R上的奇函数，
∴f（0）=0，
当x＜0时，-x＞0，
∴f（x）=-f（-x）=-（ $\frac{1}{2}$ ）^-x=-2^x．
∴函数的解析式为f（x）= $\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x＞0}\\{0，x=0}\\{-{2}^{x}，x＜0}\end{array}\right.$
（2）函数图象如图所示：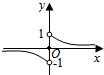
通过函数的图象可得f（x）的单调递减区间是（-∞，0）和（0，+∞）．

点评本题考查函数的解析式的求解，涉及函数的奇偶性和单调性，属基础题．

练习册系列答案

课时精练与精测系列答案

全易通系列答案

小学创新一点通系列答案

三点一测系列答案

小天才课时作业系列答案

一课四练系列答案

黄冈小状元满分冲刺微测验系列答案

新辅教导学系列答案

初中自主学习课时集训系列答案

阳光同学一线名师全优好卷系列答案

相关题目

7．已知f（x）=x²+1，g（x）=2^x-m，若对?x₁∈[-1，3]，?x₂∈[-1，3]，f（x₁）≥g（x₂），则实数m的取值范围是m≥-

\frac{1}{2}

$\frac{1}{2}$ ．

9．（1）若x，y都是正实数，且x+y＞2，求证：

\frac{1 + x}{y}

$\frac{1+x}{y}$ ＜2和

\frac{1 + y}{x}

$\frac{1+y}{x}$ ＜2中至少有一个成立．
（2）已知a、b、c∈R⁺，求证：

\sqrt{\frac{a^{2} + b^{2} + c^{2}}{3}}

$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{3}}$ ≥

\frac{a + b + c}{3}

$\frac{a+b+c}{3}$ ．

6．设函数f（x）定义在（0，+∞）上，f（1）=0，导函数f′（x）=

\frac{1}{x}

$\frac{1}{x}$ ，g（x）=f（x）+f′（x）
（1）求g（x）的单调区间和最小值；
（2）讨论g（x）与g（

\frac{1}{x}

$\frac{1}{x}$ ）的大小关系；
（3）求a的取值范围，使得g（a）-g（x）＜

\frac{1}{a}

$\frac{1}{a}$ 对任意x＞0成立．

13．先将y=sinx的图象向右平移

\frac{π}{5}

$\frac{π}{5}$ 个单位，再变化各点的横坐标（纵坐标不变），得到最小正周期为

\frac{2 π}{3}

$\frac{2π}{3}$ 的函数y=sin（ωx+φ）（其中ω＞0）的图象，则ω=3，φ=-

\frac{π}{5}

$\frac{π}{5}$ ．

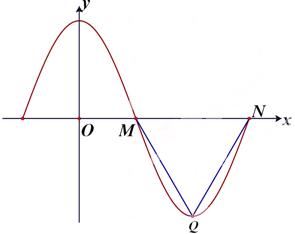函数f（x）=Acosωx（A＞0，ω＞0）部分图象如图所示，其中M、N（12，0）、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点，且△MQN是等边三角形．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若f（x₀+2）=

\sqrt{3}

$\sqrt{3}$ ，求sin

\frac{π}{4}

$\frac{π}{4}$ x₀的值．

10．在半径为8cm的圆中，

\frac{5 π}{3}

$\frac{5π}{3}$ 的圆心角所对的弧长（　　）

\frac{400 π}{3} c m

$\frac{400π}{3}cm$

\frac{20 π}{3} c m

$\frac{20π}{3}cm$

\frac{200 π}{3} c m

$\frac{200π}{3}cm$

\frac{40 π}{3} c m

$\frac{40π}{3}cm$

7．若点O是△ABC所在平面内的一点，且满足|

\vec{O B}

$\overrightarrow{OB}$ -

\vec{O C}

$\overrightarrow{OC}$ |=|

\vec{O B}

$\overrightarrow{OB}$ +

\vec{O C}

$\overrightarrow{OC}$ -2

\vec{O A}

$\overrightarrow{OA}$ |，则△ABC的形状为直角三角形．

8．已知数据x₁，x₂，…，x_n的平均数是

\bar{x}

$\overline{x}$ ，求数据ax₁+p，ax₂+p，…，ax_n+p的平均数．