题目内容
14.已知角θ的终边经过点P(3t,-4t),t≠0,求sinθ,cosθ,tanθ分析 由题意可得x=3t,y=4t,得r=$\sqrt{{{(3t)}^2}+{{(4t)}^2}}$=5|t|,再利用任意角的三角函数的定义,分类讨论求得sinθ,cosθ,tanθ的值.
解答 解:由题意可得x=3t,y=4t,得r=$\sqrt{{{(3t)}^2}+{{(4t)}^2}}$=5|t|.
当t>0时,r=5t.因此$sinθ=-\frac{4}{5},cosθ=\frac{3}{5},tanθ=-\frac{4}{3}$;
当t<0时,r=-5t.因此$sinθ=\frac{4}{5},cosθ=-\frac{3}{5},tanθ=-\frac{4}{3}$.
点评 本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
2.已知函数f(x)=$\frac{1}{2}$mx2+lnx-2x在定义域内是增函数,则实数m的取值范围为( )
| A. | (-∞,-2] | B. | (-∞,-1] | C. | [0,+∞) | D. | [1,+∞) |
19.若集合A={1,m2},B={3,4},则“m=2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.在△ABC中,若b=1,$c=\sqrt{3}$,B=30°,则a=( )
| A. | 2 | B. | 1 | C. | 1或2 | D. | 2或$\sqrt{3}$ |
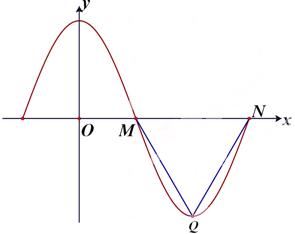 函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.
函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.