在等比数列{an}中.已知S2n=60.S3n=120.则Sn=60+$30\sqrt{5}$．题目和参考答案——青夏教育精英家教网——

题目内容

13．在等比数列{a_n}中，已知S_2n=60，S_3n=120，则S_n=60+$30\sqrt{5}$．

分析由等比数列的性质得：S_n，S_2n-S_n，S_3n-S_2n成等比数列，将条件代入可得S_n的方程求解即可．

解答解：由等比数列的性质可得：S_n，S_2n-S_n，S_3n-S_2n成等比数列，
∴（S_2n-S_n）²=S_n•（S_3n-S_2n），则（60-S_n）²=S_n•（120-60），
化简得${{S}_{n}}^{2}-180{S}_{n}+3600=0$，解得S_n=60+$30\sqrt{5}$或60-$30\sqrt{5}$（舍去），
故答案为：60+$30\sqrt{5}$．

点评本题考查等比数列前n项和的性质，属基础题．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

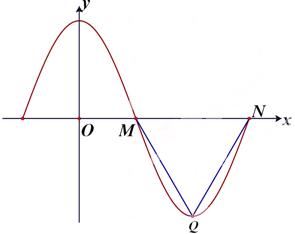函数f（x）=Acosωx（A＞0，ω＞0）部分图象如图所示，其中M、N（12，0）、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点，且△MQN是等边三角形．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若f（x₀+2）=$\sqrt{3}$，求sin$\frac{π}{4}$x₀的值．

4．在△ABC中，若b=1，$c=\sqrt{3}$，B=30°，则a=（　　）

1．设函数f（x）是定义在R上的偶函数，且f（1+x）=f（1-x）对任意的x∈R恒成立，且当x∈[0，1]时，f（x）=x²．
（1）求证：f（x）是以2为周期的函数（不需要证明2是f（x）的最小正周期）；
（2）对于整数k，当x∈[2k-1，2k+1]时，求函数f（x）的解析式；
（3）对于整数k，记M_k={a|f（x）=ax在x∈[2k-1，2x+1]有两个不等的实数根}，求集合M₂₀₁₅．

8．已知数据x₁，x₂，…，x_n的平均数是$\overline{x}$，求数据ax₁+p，ax₂+p，…，ax_n+p的平均数．

18．等比数列{a_n}的各项均为正数，且$2{a_1}+3{a_2}=1，{a_3}^2=9{a_2}{a_6}$．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n=|10+2log₃a_n|，求数列{b_n}的前n项和S_n；
（Ⅲ）设${c_n}={（{{{log}_3}{a_n}}）^2}$，求证：$\frac{1}{c_1}+\frac{1}{c_2}+\frac{1}{c_3}+…+\frac{1}{c_n}＜\frac{7}{4}$．

5．函数y=cosx|tanx|（-$\frac{π}{2}$＜x＜$\frac{π}{2}}$）的大致图象是（　　）

2．根据奇数原理，排列数A${\;}_{n}^{m}$有如下性质：A${\;}_{n+1}^{m}$=A${\;}_{n}^{m}$+mA${\;}_{n}^{m-1}$，据此类比，组合数C${\;}_{n}^{m}$具有的相应性质是：C${\;}_{n+1}^{m}$=C${\;}_{n}^{m}$+${C}_{n}^{m-1}$．

3．已知f（x）是定义在R上的奇函数，对任意x∈R，都有f（x+4）=f（x），若f（-3）=6，则f（2015）=-6．