题目内容
12.已知圆C:x2+y2+2x-4y+3=0,设点A(0,a)(a>0),若圆C上存在点M,使MA=$\sqrt{2}$MO,则a的取值范围$\sqrt{3}$≤a≤4+$\sqrt{19}$.分析 设M(x0,y0),运用两点的距离公式,化简整理可得M在以(-1,2)为圆心,$\sqrt{2}$为半径的圆上,则由两圆有公共点的条件可得圆心距离介于半径之和与半径之差的绝对值之间,解不等式即可得到r的范围.
解答 解:圆C:x2+y2+2x-4y+3=0,即圆C:(x+1)2+(y-2)2=2,表示以C(-1,2)为圆心、半径等于$\sqrt{2}$的圆.
设M(x0,y0),则由MA=$\sqrt{2}$MO,A(0,a),O(0,0),
可得(x0-0)2+(y0-a)2=2(x02+y02),即3x02+3y02+2ay0-a2=0,即x02+(y0+a)2 =2a2.
则M在以(0,-a)为圆心,r=$\sqrt{2}$a为半径的圆上.
又点M在圆C上,则这两个圆有交点,即圆心之间的距离d满足:|r-$\sqrt{2}$|≤d≤r+$\sqrt{2}$,
即|$\sqrt{2}$a-$\sqrt{2}$|≤$\sqrt{{(0+1)}^{2}{+(-a-2)}^{2}}$≤$\sqrt{2}$a+$\sqrt{2}$,即$\left\{\begin{array}{l}{{(\sqrt{2}a-\sqrt{2})}^{2}≤1{+(a+2)}^{2}}\\{1{+(a+2)}^{2}{≤(\sqrt{2}a+\sqrt{2})}^{2}}\end{array}\right.$,
求得$\sqrt{3}$≤a≤4+$\sqrt{19}$,
故答案为:$\sqrt{3}≤a≤4+\sqrt{19}$.
点评 本题考查圆的方程的求法,考查圆与圆的位置关系的判断,考查不等式的解法,属于中档题.

练习册系列答案
相关题目
2.已知函数f(x)=$\frac{1}{2}$mx2+lnx-2x在定义域内是增函数,则实数m的取值范围为( )
| A. | (-∞,-2] | B. | (-∞,-1] | C. | [0,+∞) | D. | [1,+∞) |
17.某人月初0元购入一部5000元的手机,若采用分期付款的方式每月月底等额还款,分l0个月还清,月利率0.1%按复利计算,则他每月应还款(1.011.00110≈1.01)( )
| A. | 500元 | B. | 505元 | C. | 510元 | D. | 515元 |
4.在△ABC中,若b=1,$c=\sqrt{3}$,B=30°,则a=( )
| A. | 2 | B. | 1 | C. | 1或2 | D. | 2或$\sqrt{3}$ |
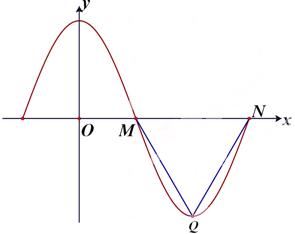 函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.
函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.