题目内容
如果两个平面分别平行于第三个平面,那么这两个平面的位置关系( )
| A.平行 | B.相交 | C.异面 | D.以上都不对 |
设平面α∥平面γ,平面β∥平面γ,则平面α∥平面β.证明如下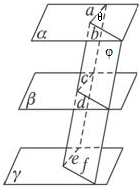 :
:
作平面θ分别与平面α、β、γ相交于直线a、c、e,
再作与平面θ相交的平面φ,分别与平面α、β、γ相交于直线b、d、f,如图所示.
∵平面α∥平面γ,平面θ∩平面α=a,平面θ∩平面γ=e,
∴a∥e,同理可得c∥e,
∴a∥c,
∵a?α,c?α,∴c∥α
同理可得b∥d,结合b?α,d?α,可得d∥α,
∵c、d是平面β内的相交直线,
∴平面β∥平面α,即平面α∥平面β.
综上所述,如果两个平面分别平行于第三个平面,那么这两个平面互相平行.
故选:A
 :
:作平面θ分别与平面α、β、γ相交于直线a、c、e,
再作与平面θ相交的平面φ,分别与平面α、β、γ相交于直线b、d、f,如图所示.
∵平面α∥平面γ,平面θ∩平面α=a,平面θ∩平面γ=e,
∴a∥e,同理可得c∥e,
∴a∥c,
∵a?α,c?α,∴c∥α
同理可得b∥d,结合b?α,d?α,可得d∥α,
∵c、d是平面β内的相交直线,
∴平面β∥平面α,即平面α∥平面β.
综上所述,如果两个平面分别平行于第三个平面,那么这两个平面互相平行.
故选:A

练习册系列答案
相关题目