题目内容
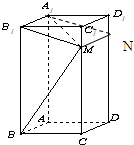
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,且∠BAC=90°,且AB=AA1,D,E,F分别为B1A,C1C,BC的中点.
(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求证:B1F⊥平面AEF;
(Ⅲ)求二面角A-EB1-F的大小.

(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求证:B1F⊥平面AEF;
(Ⅲ)求二面角A-EB1-F的大小.

证明:(Ⅰ)设AB的中点为G,连接DG,CG
∵D是A1B的中点
∴DG∥A1A且DG=
A1A
∵E是C1C的中点
∴CE∥A1A且CE=
A1A
∴CE∥DG且CE=DG
∴CEDG是平行四边形
∴DE∥GC
∵DE?平面ABC,GC?平面ABC
∴DE∥平面ABC(4分)
(Ⅱ)∵△ABC为等腰直角三角形,∠BAC=90°,且F是BC的中点
∴AF⊥BC
∵平面ABC⊥平面BCC1B1
∴AF⊥平面BCC1B1
∴AF⊥B1F(6分)
设AB=AA1=2
则在B1FE中,B1F=
,
则EF=
,B1E=3
∴B1E2=B1F2+EF2=9
∴△B1FE是直角三角形,
∴B1F⊥EF(8分)
∵AF∩EF=F
∴B1F⊥平面AEF(9分)
(Ⅲ)分别以AB,AC,AA1为x,y,z轴建立空间直角坐标系A-xyz,
设AB=AA1=2,则设A(0,0,0),B1(2,0,2),E(0,2,1),F(1,1,0),D(1,0,1)
∵AF⊥平面BCC1B1
∴面B1FE的法向量为
=(1,1,0),(10分)
设平面AB1E的法向量为
=(x,y,z)
∵
=(0,2,1),
=(1,0,1)
∴
•
=0,
•
=0
∴2y+z=0,,x+z=0,
不妨设z=-2,可得
=(2,1,-2)(12分)
∴cos<
,
>=
=
=
(13分)
∵二面角A-EB1-F是锐角
∴二面角A-EB1-F的大小45°(14分)
∵D是A1B的中点

∴DG∥A1A且DG=
| 1 |
| 2 |
∵E是C1C的中点
∴CE∥A1A且CE=
| 1 |
| 2 |
∴CE∥DG且CE=DG
∴CEDG是平行四边形
∴DE∥GC
∵DE?平面ABC,GC?平面ABC
∴DE∥平面ABC(4分)
(Ⅱ)∵△ABC为等腰直角三角形,∠BAC=90°,且F是BC的中点
∴AF⊥BC
∵平面ABC⊥平面BCC1B1
∴AF⊥平面BCC1B1
∴AF⊥B1F(6分)
设AB=AA1=2
则在B1FE中,B1F=
| 6 |
则EF=
| 3 |
∴B1E2=B1F2+EF2=9
∴△B1FE是直角三角形,
∴B1F⊥EF(8分)
∵AF∩EF=F
∴B1F⊥平面AEF(9分)
(Ⅲ)分别以AB,AC,AA1为x,y,z轴建立空间直角坐标系A-xyz,
设AB=AA1=2,则设A(0,0,0),B1(2,0,2),E(0,2,1),F(1,1,0),D(1,0,1)
∵AF⊥平面BCC1B1
∴面B1FE的法向量为
| AF |
设平面AB1E的法向量为
| n |
∵
| AE |
| AD |
∴
| AE |
| n |
| AD |
| n |
∴2y+z=0,,x+z=0,
不妨设z=-2,可得
| n |
∴cos<
| n |
| AF |
| ||||
|
|
| 3 | ||
3
|
| ||
| 2 |
∵二面角A-EB1-F是锐角
∴二面角A-EB1-F的大小45°(14分)

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目