题目内容

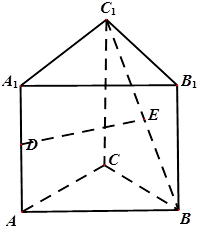
正方体ABCD-A1B1C1D1中，E为A1C1的中点，则直线CE垂直于（　　）
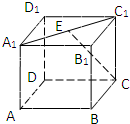
A．直线ACB．直线B1D1C．直线A1D1D．直线A1A

如图，直线CE垂直于直线B1D1

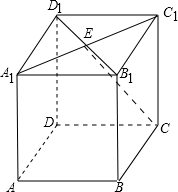
事实上，∵AC1为正方体，∴A1B1C1D1为正方形，连结B1D1，
又∵E为为A1C1的中点，∴E∈B1D1．
∴B1D1⊥C1E，
CC1⊥面A1B1C1D1，∴CC1⊥B1D1，
又CC1∩C1E=C1，∴B1D1⊥面CC1E，而CE?面CC1E，∴直线CE垂直于直线B1D1
故选：B．
练习册系列答案
相关题目
如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6．D、E分别是AC、AB上的点，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD，如图2．
（1）求证：BC∥平面A1DE；
（2）求证：BC⊥平面A1DC；
（3）当D点在何处时，A1B的长度最小，并求出最小值．
如果两个平面分别平行于第三个平面，那么这两个平面的位置关系（　　）
A．平行B．相交C．异面D．以上都不对
如图，在三棱柱ABC-A1B1C1中，△ABC为等边三角形，侧棱AA1⊥平面ABC，AB=2，AA1=2
3
，D、E分别为AA1、BC1的中点．
（Ⅰ）求证：DE⊥平面BB1C1C；
（Ⅱ）求三棱锥C-BC1D的体积．
P是平行四边形ABCD所在平面外的一点，若P到四边的距离都相等，则四边形ABCD（　　）
A．是正方形B．是长方形
C．有一个内切圆D．有一个外接圆
如图在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，垂足为点A，PA=AB=2，点M，N分别是PD，PB的中点．
（I）求证：PB∥平面ACM；
（II）求证：MN⊥平面PAC；
（III）求四面体A-MBC的体积．
如图所示，在长方体ABCD-A1B1C1D1中，AB=1，BC=2，CC1=5，M为棱CC1上一点．
（1）若C1M=
3
2
，求异面直线A1M和C1D1所成角的正切值；
（2）是否存在这样的点M使得BM⊥平面A1B1M？若存在，求出C1M的长；若不存在，请说明理由．
如图，在底面为菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=
2
a，点E在PD上，且PE：ED=2：1．
（1）求证：PA⊥平面ABCD；
（2）求面EAC与面DAC所成的二面角的大小．
设α、β为两个不同的平面，直线l?α，则“l⊥β”是“α⊥β”成立的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网