题目内容
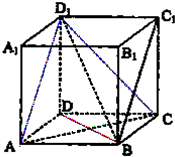
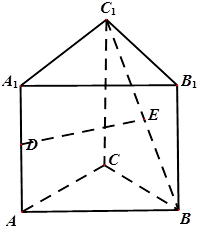
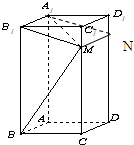
如图,在正方体ABCD-A1B1C1D1中,E,F,M分别是BB1,CC1与AB的中点,
(1)求证:AE∥平面A1DF;
(2)求证:A1M⊥平面AED;
(3)正方体棱长为2,求三棱锥A1-DEF的体积.
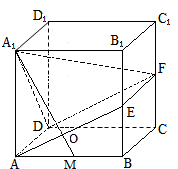
(1)求证:AE∥平面A1DF;
(2)求证:A1M⊥平面AED;
(3)正方体棱长为2,求三棱锥A1-DEF的体积.

证明:(1)∵E,F分别是BB1,CC1的中点
∴EF∥BC,EF=BC
又∵AD∥BC,AD=BC
∴EF∥AD,EF=AD
∴四边形AEFD为平行四DF边形,
∴AE∥DF
∵AE?平面A1DF,DF?平面A1DF
∴AE∥平面A1DF
(2)由正方体的几何特征可得AD⊥平面ABB1A1,
又∵A1M?平面ABB1A1,
∴AD⊥A1M
在正方形ABB1A1中,E,M分别是BB1与AB的中点,
∴△AA1M≌△BAE
∴∠BAE=∠AA1M
∵∠BAE+∠AA1O=90°
∴AA1M+AA1O=90°
∴A1M⊥AE
∵AD∩AE=A,AD,AE?平面AED
∴A1M⊥平面AED;
(3)∵正方体棱长为2,
∴三棱锥A1-DEF的体积
VA1-DEF=VA1-ADE=VD-A1AE=
•S△A1AE•AD=
•
•2•2•2=

∴EF∥BC,EF=BC
又∵AD∥BC,AD=BC
∴EF∥AD,EF=AD
∴四边形AEFD为平行四DF边形,
∴AE∥DF
∵AE?平面A1DF,DF?平面A1DF
∴AE∥平面A1DF
(2)由正方体的几何特征可得AD⊥平面ABB1A1,
又∵A1M?平面ABB1A1,
∴AD⊥A1M
在正方形ABB1A1中,E,M分别是BB1与AB的中点,
∴△AA1M≌△BAE
∴∠BAE=∠AA1M
∵∠BAE+∠AA1O=90°
∴AA1M+AA1O=90°
∴A1M⊥AE
∵AD∩AE=A,AD,AE?平面AED
∴A1M⊥平面AED;
(3)∵正方体棱长为2,
∴三棱锥A1-DEF的体积
VA1-DEF=VA1-ADE=VD-A1AE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |


练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目