题目内容
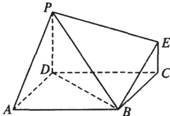
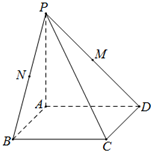
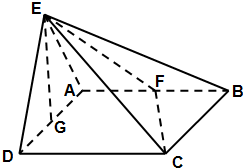
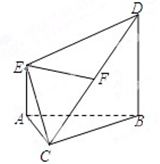
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F在CD上(不含C,D两点)
(1)求多面体ABCDE的体积;
(2)若F为CD中点,求证:EF⊥面BCD;
(3)当
的值为多少时,能使AC∥平面EFB,并给出证明.
(1)求多面体ABCDE的体积;
(2)若F为CD中点,求证:EF⊥面BCD;
(3)当
| DF |
| FC |

(1)过C作CH⊥AB于H,
∵AE⊥平面ABC,AE?平面AEDB,∴平面AEDB⊥平面ABC,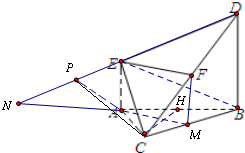
∵平面AEDB∩平面ABC=AB,CH?平面ABC,CH⊥AB
∴CH⊥平面ABDE,可得CH就是四棱锥C-ABED的高
∵梯形ABDE的面积为S=
(AE+BD)•AB=3,CH=
AB=
∴多面体ABCDE的体积为:V=
SABDE×CH=
-------(6分)
(2)取BC中点M,连接AM、FM,
∵BD∥AE,AE⊥平面ABC,可得BD⊥平面ABC,∴BD⊥AM
∵正△ABC中,AM⊥CB,CB、BD是平面BCD内的相交直线,∴AM⊥平面BCD
∵AE∥BD且AE=
BD,在△BCD中,FM∥BD且FM=
BD
∴AE∥FM且AE=FM,由此可得四边形AEFM是平行四边形,可得EF∥AM
∴EF⊥平面BCD----------(10分)
(3)延长BA交DE延长线于N,连接BE,过A作AP∥BE,交DE于P,连接PC.
则当DF:FC=2:1时,AC∥平面EFB,证明如下
∵
=
=
,∴PC∥EF
∵PC?平面EFB,EF?平面EFB,∴PC∥平面EFB,同理可证AP∥平面EFB
∵PC、AP是平面PAC内的相交直线,∴平面PAC∥平面EFB
∵AC?平面PAC,∴AC∥平面EFB
即当
的值为2时,能使AC∥平面EFB---------------------(16分)
∵AE⊥平面ABC,AE?平面AEDB,∴平面AEDB⊥平面ABC,

∵平面AEDB∩平面ABC=AB,CH?平面ABC,CH⊥AB
∴CH⊥平面ABDE,可得CH就是四棱锥C-ABED的高
∵梯形ABDE的面积为S=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴多面体ABCDE的体积为:V=
| 1 |
| 3 |
| 3 |
(2)取BC中点M,连接AM、FM,
∵BD∥AE,AE⊥平面ABC,可得BD⊥平面ABC,∴BD⊥AM
∵正△ABC中,AM⊥CB,CB、BD是平面BCD内的相交直线,∴AM⊥平面BCD
∵AE∥BD且AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE∥FM且AE=FM,由此可得四边形AEFM是平行四边形,可得EF∥AM
∴EF⊥平面BCD----------(10分)
(3)延长BA交DE延长线于N,连接BE,过A作AP∥BE,交DE于P,连接PC.
则当DF:FC=2:1时,AC∥平面EFB,证明如下
∵
| DE |
| EP |
| 2 |
| 1 |
| DF |
| FC |
∵PC?平面EFB,EF?平面EFB,∴PC∥平面EFB,同理可证AP∥平面EFB
∵PC、AP是平面PAC内的相交直线,∴平面PAC∥平面EFB
∵AC?平面PAC,∴AC∥平面EFB
即当
| DF |
| FC |

练习册系列答案
相关题目