题目内容

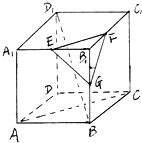
如图，在正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面PAO？
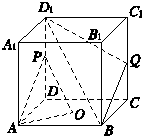
当Q为CC1的中点时，平面D1BQ∥平面PAO．
∵Q为CC1的中点，P为DD1的中点，∴QB∥PA．
连接DB．∵P、O分别为DD1、DB的中点，
∴D1B∥PO．又D1B?平面PAO，QB?平面PAO，∴D1B∥面PAO．
再由QB∥面PAO，且 D1B∩QB=B，∴平面D1BQ∥平面PAO．
练习册系列答案
相关题目
如图，在三棱锥S-ABC中，平面SAB⊥平面SBC，AB⊥BC，AS=AB，过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．求证：
（1）平面EFG∥平面ABC；
（2）BC⊥SA．
如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6．D、E分别是AC、AB上的点，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD，如图2．
（1）求证：BC∥平面A1DE；
（2）求证：BC⊥平面A1DC；
（3）当D点在何处时，A1B的长度最小，并求出最小值．
如图，在四棱柱ABCD-A1B1C1D1中，D1D⊥底面ABCD，底面ABCD是正方形，且AB=1，D1D=
2
，E、F、G分别A1B1、B1C1、BB1的中点．
（1）求直线D1B与平面ABCD所成角的大小．
（2）求证：AC∥平面EGF．
如图，在直三棱柱ABC-A1B1C1中，E，F分别是A1B，A1C的中点，点D在B1C1上，A1D⊥B1C．求证：
（1）EF∥平面ABC；
（2）平面A1FD⊥平面BB1C1C．
正三棱柱ABC-A1B1C1中，M、N分别为A1B1、AB的中点．
①求证：平面A1NC∥平面BMC1；
②若AB=AA1，求BM与AC所成角的余弦值．
如果两个平面分别平行于第三个平面，那么这两个平面的位置关系（　　）
A．平行B．相交C．异面D．以上都不对
如图，在三棱柱ABC-A1B1C1中，△ABC为等边三角形，侧棱AA1⊥平面ABC，AB=2，AA1=2
3
，D、E分别为AA1、BC1的中点．
（Ⅰ）求证：DE⊥平面BB1C1C；
（Ⅱ）求三棱锥C-BC1D的体积．
如图，在底面为菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=
2
a，点E在PD上，且PE：ED=2：1．
（1）求证：PA⊥平面ABCD；
（2）求面EAC与面DAC所成的二面角的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网