题目内容
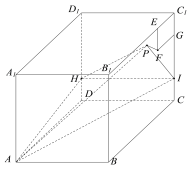
【题目】如图所示,正方体ABCD﹣A1B1C1D1棱长为4,点![]() 在棱
在棱![]() 上,点
上,点![]() 在棱
在棱![]() 上,且
上,且![]() .在侧面
.在侧面![]() 内以
内以![]() 为一个顶点作边长为1的正方形
为一个顶点作边长为1的正方形![]() ,侧面
,侧面![]() 内动点
内动点![]() 满足到平面
满足到平面![]() 距离等于线段
距离等于线段![]() 长的
长的![]() 倍,则当点
倍,则当点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积的最小值是( )
的体积的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
建立空间直角坐标系,求出P的轨迹方程,确定三棱锥A﹣HPI的体积最小时,P的坐标,即可得出结论.
解:建立空间直角坐标系,如图所示
设P(x,4,z),则F(1,4,3),N(0,4,z),且4≥x≥0,4≥z≥0;
∵PN![]() PF,∴
PF,∴![]() =2(x﹣1)2+2(z﹣3)2,
=2(x﹣1)2+2(z﹣3)2,
化简得![]() +(z﹣3)2
+(z﹣3)2![]() ,P点轨迹为椭圆,
,P点轨迹为椭圆,
∴三棱锥A﹣HPI的体积最小,P点处的切线平行于BI,
∵A(4,0,0),H(0,0,1),I(0,4,1),
∴![]() (﹣4,0,1),
(﹣4,0,1),![]() (﹣4,4,1),
(﹣4,4,1),
设平面AHI的法向量为![]() (x,y,z),则
(x,y,z),则![]() ,
,
∴![]() (1,0,4),
(1,0,4),
∵![]() (
(![]() ,4,
,4,![]() )∴P到平面AHI的距离为
)∴P到平面AHI的距离为![]()
∵![]() +(z﹣3)2
+(z﹣3)2![]()
设![]() ,
,![]()
则![]() ,
,
∴三棱锥A﹣HPI的体积的最小值是![]()
故选:B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力。某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果。例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人。
视觉 听觉 | 视觉记忆能力 | ||||
偏低 | 中等 | 偏高 | 超常 | ||
听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
中等 | 1 | 8 | 3 | b | |
偏高 | 2 | a | 0 | 1 | |
超常 | 0 | 2 | 1 | 1 | |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为![]() 。
。
(1)试确定a,b的值;
(2)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为X,求随机变量X的分布列。