题目内容
【题目】在平面直角坐标系
中，平行四边形
的周长为8，其对角线
的端点
，
.
（1）求动点
的轨迹
的方程；
（2）已知点
，记直线
与曲线的另一交点为
，直线
，
分别与直线
交于点
，
.证明：以线段
为直径的圆恒过点
.
【答案】（1）
（2）详见解析
【解析】
(1)由椭圆的定义得到点
的轨迹为以
，
为焦点的椭圆（除去长轴端点），结合椭圆的性质得到参数值；（2）将直线设为横截式，联立直线和椭圆方程，设出直线PA,PE,可得到
，
，
根据韦达定理得到结果为0，进而得到线段
为直径的圆恒过点.
（1）依题意得
∴点的轨迹为以，为焦点的椭圆（除去长轴端点）
设
的方程为
∴
，
，
∴
（2）设直线
的方程为
，
，
由
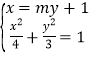得
易得
，∴
，
，
∴直线
的方程为
，直线
的方程为
∴，.
∴
，
，∴
又
∴
∴
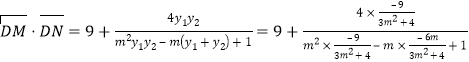
∴以线段为直径的圆恒过点.
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
