题目内容
【题目】已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3.
(1)求数列{an}的通项公式;
(2){bn}为各项非零的等差数列,其前n项和为Sn.已知S2n+1=bnbn+1,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
【答案】(1)an=2n.(2)Tn=5-![]() .
.
【解析】试题分析:
(1)由条件可求得等比数列{an}的首项![]() ,公比
,公比![]() ,根据公式可得所求.(2)由等差数列的求和公式及性质可得
,根据公式可得所求.(2)由等差数列的求和公式及性质可得![]() ,然后结合条件S2n+1=bnbn+1得bn=2n+1,于是得到
,然后结合条件S2n+1=bnbn+1得bn=2n+1,于是得到![]() ,再根据错位相减法求解可得所求数列的前n项和.
,再根据错位相减法求解可得所求数列的前n项和.
试题解析:
(1)设等比数列{an}的公比为q,
由题意知![]() ,又an>0,故可得
,又an>0,故可得![]() .
.
∴![]() .
.
(2)∵数列{bn}为等差数列,
∴![]() .
.
又S2n+1=bnbn+1,bn+1≠0,
∴bn=2n+1.
令cn=![]() ,则cn=
,则cn=![]() .
.
∴Tn=c1+c2+…+cn=![]() +
+![]() +
+![]() +…+
+…+![]() +
+![]() ,①
,①
∴![]() Tn=
Tn=![]() +
+![]() +
+![]() +…+
+…+![]() +
+![]() ,②
,②
①-②得![]() Tn=
Tn=![]() +(
+(![]() +
+![]() +…+
+…+![]() )-
)-![]()
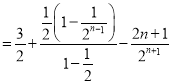
![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目