题目内容
在△ABC中,已知B(-2,0)、C(2,0),AD⊥BC于点D,△ABC的垂心为H,且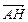 =
=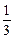
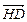 .
.
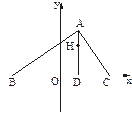
(1)求点H(x,y)的轨迹G的方程;
(2)已知P(-1,0)、Q(1,0),M是曲线G上的一点,那么 ,
,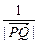 ,
, 能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
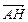 =
=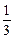
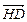 .
.
(1)求点H(x,y)的轨迹G的方程;
(2)已知P(-1,0)、Q(1,0),M是曲线G上的一点,那么
 ,
,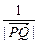 ,
, 能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.(1) G的方程为 +
+ =1(y≠0).
=1(y≠0). (2)见解析
(2)见解析
 +
+ =1(y≠0).
=1(y≠0). (2)见解析
(2)见解析(1)∵H点坐标为(x,y),则D点坐标为(x,0),
由定比分点坐标公式可知,A点的坐标为(x, y).
y).
∴ =(x+2,y),
=(x+2,y),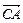 =(x-2,
=(x-2, y).
y).
由BH⊥CA知x2-4+ y2=0,即
y2=0,即 +
+  =1,
=1,
∴G的方程为 +
+ =1(y≠0).
=1(y≠0).
(2)解法一:显然P、Q恰好为G的两个焦点,
∴|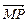 |+|
|+| |=4,|
|=4,| |=2.
|=2.
若 ,
,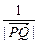 ,
, 成等差数列,则
成等差数列,则 +
+ =
= =1.
=1.
∴|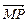 |·|
|·| |="|"
|="|" 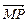 |+|
|+| |=4.
|=4.
由 可得|
可得|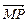 |=|
|=| |=2,
|=2,
∴M点为 +
+ =1的短轴端点.
=1的短轴端点.
∴当M点的坐标为(0,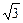 )或(0,-
)或(0,-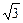 )时,
)时, ,
,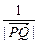 ,
, 成等差数列.
成等差数列.
解法二:设M点的坐标为(x,y),
显然P、Q恰好为 +
+  =1的两个焦点,
=1的两个焦点,
∴|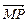 |+|
|+| |="4,|"
|="4,|"  |=2.
|=2.
∵ ,
,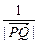 ,
, 成等差数列,
成等差数列,
∴ +
+ =
= =1.
=1.
由椭圆第二定义可得|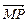 |=a+ex,|
|=a+ex,| |=a-ex,
|=a-ex,
∴ +
+ =1.解得x=0.
=1.解得x=0.
∴M点的坐标为(0,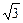 )或(0,-
)或(0,-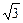 ).
).
∴当M点的坐标为(0,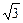 )或(0,-
)或(0,-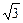 )时,
)时, ,
,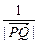 ,
, 成等差数列.
成等差数列.
由定比分点坐标公式可知,A点的坐标为(x,
 y).
y).∴
 =(x+2,y),
=(x+2,y),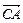 =(x-2,
=(x-2, y).
y).由BH⊥CA知x2-4+
 y2=0,即
y2=0,即 +
+  =1,
=1,∴G的方程为
 +
+ =1(y≠0).
=1(y≠0).(2)解法一:显然P、Q恰好为G的两个焦点,
∴|
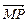 |+|
|+| |=4,|
|=4,| |=2.
|=2.若
 ,
,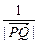 ,
, 成等差数列,则
成等差数列,则 +
+ =
= =1.
=1.∴|
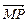 |·|
|·| |="|"
|="|" 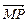 |+|
|+| |=4.
|=4.由
 可得|
可得|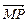 |=|
|=| |=2,
|=2,∴M点为
 +
+ =1的短轴端点.
=1的短轴端点.∴当M点的坐标为(0,
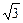 )或(0,-
)或(0,-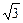 )时,
)时, ,
,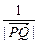 ,
, 成等差数列.
成等差数列.解法二:设M点的坐标为(x,y),
显然P、Q恰好为
 +
+  =1的两个焦点,
=1的两个焦点,∴|
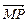 |+|
|+| |="4,|"
|="4,|"  |=2.
|=2.∵
 ,
,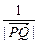 ,
, 成等差数列,
成等差数列,∴
 +
+ =
= =1.
=1.由椭圆第二定义可得|
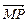 |=a+ex,|
|=a+ex,| |=a-ex,
|=a-ex,∴
 +
+ =1.解得x=0.
=1.解得x=0.∴M点的坐标为(0,
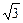 )或(0,-
)或(0,-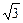 ).
).∴当M点的坐标为(0,
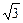 )或(0,-
)或(0,-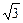 )时,
)时, ,
,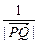 ,
, 成等差数列.
成等差数列.
练习册系列答案
相关题目
 ,1)、P2(-
,1)、P2(- ,-
,- ),求椭圆的方程.
),求椭圆的方程. ,0),则椭圆的标准方程为_________.
,0),则椭圆的标准方程为_________. d,
d, ≤d≤
≤d≤ .
. ·
· =
= ,求向量
,求向量 与
与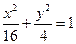 ,过点
,过点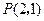 引1条弦,使它在这点平分,求此弦所在直线方程.
引1条弦,使它在这点平分,求此弦所在直线方程. .
. ,
, ,则
,则 的轨迹方程是
的轨迹方程是