题目内容
6．已知正数x，y满足xy+x+2y=6，则xy的最大值为2．分析 正数x，y满足xy+x+2y=6，可得x=$\frac{6-2y}{y+1}$＞0，解得0＜y＜3．可得xy=$\frac{y（6-2y）}{y+1}$，化简整理利用基本不等式的性质即可得出．
解答 解：∵正数x，y满足xy+x+2y=6，
∴x=$\frac{6-2y}{y+1}$＞0，解得0＜y＜3．
∴xy=$\frac{y（6-2y）}{y+1}$=$-2（y+1+\frac{4}{y+1}）+10$≤$-2×2\sqrt{（y+1）•\frac{4}{y+1}}$+10=2，当且仅当y=1（x=2）时取等号．
∴xy的最大值为2．
故答案为：2．
点评 本题考查了基本不等式的性质，考查了变形能力、推理能力，属于基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内，其中顶点P、C、Q、D分别在矩形的四条边上．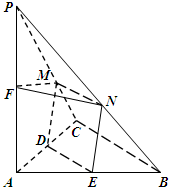
如图，在三棱锥P-ABC中，PA⊥平面ABC，2AC=2BC=PC=2，AC⊥BC，D、E、F分别为AC、AB、AP的中点，M、N分别为线段PC、PB上的动点，且有MN∥BC．
1．已知m，n是两条不同的直线，α，β，γ为三个不同的平面，则下列命题中错误的是（ ）
| A． | 若m⊥α，m⊥β，则α∥β | B． | 若m⊥α，n⊥α，则m∥n | C． | 若α∥γ，β∥γ，则α∥β | D． | 若α⊥γ，β⊥γ，则α∥β |
如图，已知AB为半圆O的直径，C为圆弧上一点，过点C作半圆的切线CF，过点A作CF的垂线，垂足为D，AD交半圆于点E，连结EC，BC，AC．