题目内容
1.已知m,n是两条不同的直线,α,β,γ为三个不同的平面,则下列命题中错误的是( )| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m⊥α,n⊥α,则m∥n | C. | 若α∥γ,β∥γ,则α∥β | D. | 若α⊥γ,β⊥γ,则α∥β |
分析 根据空间线面垂直、面面垂直、面面平行的性质定理对选项分别分析选择.
解答 解:对于A,若m⊥α,m⊥β,根据线面垂直的性质定理以及面面平行的判定定理可以得到α∥β;故a正确;
对于B,若m⊥α,n⊥α,根据线面垂直的性质定理容易得到m∥n,故B正确;
对于C,若α∥γ,β∥γ,根据面面平行的性质定理和判定定理容易得到α∥β;故D正确;
对于D,若α⊥γ,β⊥γ,则α与β可能相交;如墙角的三个面的关系;故D是错误的.
故选D.
点评 本题考查了空间线面垂直、面面垂直、面面平行的性质定理和判定定理的运用;牢固掌握运用定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.运行如下程序框图,如果输入的x∈(-∞,1],则输出的y属于( )
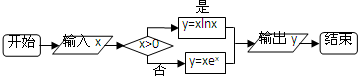

| A. | [-$\frac{1}{e}$,0] | B. | [-$\frac{1}{e}$,0) | C. | [-$\frac{1}{e}$,+∞) | D. | [-$\frac{1}{e}$,e) |
11.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线的斜率为2,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |