题目内容
18. 如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.
如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.(Ⅰ)证明:AC平分∠BAD;
(Ⅱ)若AB=3,DE=$\frac{3}{4}$,求△ABC的面积.
分析 (Ⅰ)证明∠BAC=∠CAD,即可证明:AC平分∠BAD;
(Ⅱ)证明△DCE∽△CAB,则$\frac{DE}{CE}=\frac{CB}{AB}$,求出BC,即可求△ABC的面积.
解答 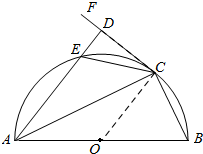 (Ⅰ)证明:由CD为半圆O的切线,根据弦切角定理得∠DCA=∠CBA,
(Ⅰ)证明:由CD为半圆O的切线,根据弦切角定理得∠DCA=∠CBA,
又因为∠CDA=∠BCA=90°,得∠BAC=∠CAD,
所以AC平分∠BAD;…(5分)
(Ⅱ)解:由CD为半圆O的切线,根据弦切角定理得∠DCE=∠CDA,
又因为∠CAD=∠CAB,所以∠DCE=∠CAB,
可得△DCE∽△CAB,则$\frac{DE}{CE}=\frac{CB}{AB}$,
又因为EC=BC,AB=3,DE=$\frac{3}{4}$,
所以BC=$\frac{3}{2}$,即S△ABC$\frac{9\sqrt{3}}{8}$.…(10分)
点评 本题考查弦切角定理,考查三角形相似的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
7.“α为第一象限角”是“$\frac{sinα}{cosα}$+$\frac{cosα}{sinα}$≥2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |