题目内容
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元
【答案】D
【解析】
设该企业生产甲产品x吨,乙产品y吨,利润为z万元,根据图表写出约束条件以及目标函数,从而转化为线性规划问题,利用数形结合即可求出最大利润.
设该企业生产甲产品x吨,乙产品y吨,利润为z万元,
则约束条件为![]() ,且x,y≥0,目标函数z=3x+4y,
,且x,y≥0,目标函数z=3x+4y,
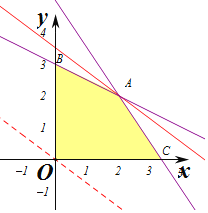
作出不等式组对应的平面区域如图:
由z=3x+4y,得y=-![]() x+
x+![]() ,平移直线y=-
,平移直线y=-![]() x+
x+![]() ,
,
由图象知当直线y=-![]() x+
x+![]() 经过点A时,y=-
经过点A时,y=-![]() x+
x+![]() 的截距最大,此时z最大,
的截距最大,此时z最大,
由![]() 即A(2,2),此时z=3×2+4×2=6+8=14(万元),
即A(2,2),此时z=3×2+4×2=6+8=14(万元),
即该企业生产甲产品2吨,乙产品2吨,利润为14万元,
故选:D.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目