Question

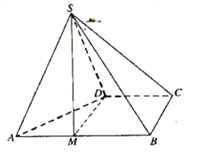
【题目】如图在直三棱柱ABC A1B1C1中，已知AC⊥BC，BC＝CC1，设AB1的中点为D，B1C∩BC1＝E.

（1）求证：DE∥平面AA1C1C；

(2) 求证：BC1⊥AB1；

（3）设AC=BC＝CC1 =1,求锐二面角A- B1C- A1的余弦值。

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）由DE是△B1AC中位，线易知DE∥AC，从而DE∥平面AA1C1C；（2）先证AC⊥平面BCC1B1，得BC1⊥AC，又因为BC1⊥B1C，所以BC1⊥平面B1AC，所以BC1⊥AB1；（3）先求出点A1到平面B1AC的距离，再求出点A1到交线B1C的距离，，转化为余弦值即可.

证明：(1)由题意知，E为B1C的中点，

又D为AB1的中点，因此DE∥AC.

又因为DE平面AA1C1C，AC平面AA1C1C，

所以DE∥平面AA1C1C.

(2)因为三棱柱ABC A1B1C1是直三棱柱，

所以CC1⊥平面ABC.

因为AC平面ABC，所以AC⊥CC1.

又因为AC⊥BC，CC1平面BCC1B1，

BC平面BCC1B1，BC∩CC1＝C，

所以AC⊥平面BCC1B1.

又因为BC1平面BCC1B1，所以BC1⊥AC.

因为BC＝CC1，所以矩形BCC1B1是正方形，因此BC1⊥B1C.

因为AC，B1C平面B1AC，AC∩B1C＝C，所以BC1⊥平面B1AC.

又因为AB1平面B1AC，所以BC1⊥AB1.

（3）因为A1C1∥AC，AC平面B1AC，A1C1平面B1AC

所以A1C1∥平面B1AC

所以点A1到平面B1AC与点C1到平面B1AC的距离相等，且

又因为在△A1B1C中，A1B1=A1C=B1C=，

所以点A1到直线B1C的距离

所以锐二面角A- B1C- A1的正弦值

所以锐二面角A- B1C- A1的正弦值