题目内容
【题目】已知函数![]() (
(![]() )在同一半周期内的图象过点
)在同一半周期内的图象过点![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 为坐标原点,
为坐标原点, ![]() 为函数
为函数![]() 图象的最高点,
图象的最高点, ![]() 为函数
为函数![]() 的图象与
的图象与![]() 轴的正半轴的交点,
轴的正半轴的交点, ![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求![]() 的值;
的值;
(2)将![]() 绕原点
绕原点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() ,得到
,得到![]() ,若点
,若点![]() 恰好落在曲线
恰好落在曲线![]() (
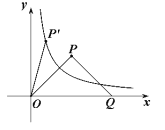
(![]() )上(如图所示),试判断点
)上(如图所示),试判断点![]() 是否也落在曲线
是否也落在曲线![]() (
(![]() )上,并说明理由.
)上,并说明理由.
【答案】(1)2;(2)见解析.
【解析】试题分析:(1)由已知利用周期公式可求最小正周期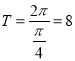 ,由题意可求Q坐标为(4,0).P坐标为(2,
,由题意可求Q坐标为(4,0).P坐标为(2, ![]() ),结合△OPQ为等腰直角三角形,即可得解
),结合△OPQ为等腰直角三角形,即可得解![]() ;
;
(2)由(Ⅰ)知, ![]() ,
, ![]() ,可求点P′,Q′的坐标,由点
,可求点P′,Q′的坐标,由点![]() 在曲线
在曲线![]() ,(x>0)上,利用倍角公式,诱导公式可求
,(x>0)上,利用倍角公式,诱导公式可求![]() ,又结合
,又结合![]() ,,可求
,,可求![]() 的值,由于
的值,由于![]() ,即可证明点Q′不落在曲线
,即可证明点Q′不落在曲线![]() (
(![]() )上.
)上.
试题解析:
(1)因为函数![]() (
(![]() )的最小正周期
)的最小正周期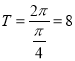 ,所以函数
,所以函数![]() 的半周期为
的半周期为![]() ,
,
所以![]() ,即有
,即有![]() 坐标为
坐标为![]() ,
,
又因为![]() 为函数
为函数![]() 图象的最高点,所以点
图象的最高点,所以点![]() 的坐标为
的坐标为![]() .
.
又因为![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() .
.
(2)点![]() 不落在曲线
不落在曲线![]() (
(![]() )上,理由如下:
)上,理由如下:
由(1)知, ![]() ,
, ![]()
所以点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() .
.
因为点![]() 在曲线
在曲线![]() (
(![]() )上,所以
)上,所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() .
.
又![]() .所以点
.所以点![]() 不落在曲线
不落在曲线![]() (
(![]() )上.
)上.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目